From Newton's second law,
![]() (introduced in Eq.(B.1)),
we can use d'Alembert's idea of virtual work to derive the
formula for the kinetic energy of a mass given its speed
(introduced in Eq.(B.1)),
we can use d'Alembert's idea of virtual work to derive the
formula for the kinetic energy of a mass given its speed
![]() .
Let
.
Let ![]() denote a small (infinitesimal) displacement of the mass in
the
denote a small (infinitesimal) displacement of the mass in
the ![]() direction. Then we have, using the calculus of differentials,
direction. Then we have, using the calculus of differentials,
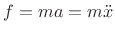
Thus, by Newton's second law, a differential of work ![]() applied to a
mass
applied to a
mass ![]() by force
by force ![]() through distance
through distance ![]() boosts the kinetic energy
of the mass by
boosts the kinetic energy
of the mass by
![]() . The kinetic energy of a mass moving at
speed
. The kinetic energy of a mass moving at
speed ![]() is then given by the integral of all such differential
boosts from 0 to
is then given by the integral of all such differential
boosts from 0 to ![]() :
:

where
The quantity ![]() is classically called the virtual work
associated with force
is classically called the virtual work
associated with force ![]() , and
, and ![]() a virtual displacement
[548].
a virtual displacement
[548].