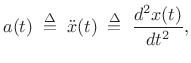Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Newton's Laws of Motion
Perhaps the most heavily used equation in physics is Newton's second
law of motion:
That is, when a force is applied to a mass, the mass experiences an
acceleration proportional to the applied force. Denoting the mass by
 , force at time
, force at time 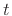 by
by 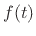 , and acceleration by
, and acceleration by
we have
 |
(B.1) |
In this formulation, the applied force 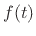 is considered positive
in the direction of positive mass-position
is considered positive
in the direction of positive mass-position 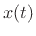 . The force
. The force 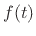 and acceleration
and acceleration 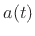 are, in general, vectors in
three-dimensional space
are, in general, vectors in
three-dimensional space
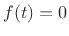 . In other words, force and
acceleration are generally vector-valued functions of time
. In other words, force and
acceleration are generally vector-valued functions of time 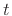 . The
mass
. The
mass  is a scalar quantity, and can be considered a measure of the
inertia of the physical system (see §B.1.1 below).
is a scalar quantity, and can be considered a measure of the
inertia of the physical system (see §B.1.1 below).
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]