Kinetic energy is energy associated with motion. For example, when a spring uncompresses and accelerates a mass, as in the configuration of Fig.B.2, work is performed on the mass by the spring, and we say that the potential energy of the spring is converted to kinetic energy of the mass.
Suppose in Fig.B.2 we have an initial spring compression
by ![]() meters at time
meters at time ![]() , and the mass velocity is zero at
, and the mass velocity is zero at
![]() . Then from the equation of motion Eq.(B.5), we can calculate
when the spring returns to rest (
. Then from the equation of motion Eq.(B.5), we can calculate
when the spring returns to rest (![]() ). This first happens at the
first zero of
). This first happens at the
first zero of
![]() , which is time
, which is time
![]() . At this time, the velocity,
given by the time-derivative of Eq.(B.5),
. At this time, the velocity,
given by the time-derivative of Eq.(B.5),
can be evaluated at
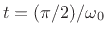
and we see that if we multiply
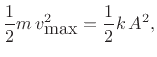
which is the initial potential energy stored in the spring. We require this result. Therefore, the kinetic energy of a mass must be given by
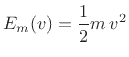
in order that the kinetic energy of the mass when spring compression is zero equals the original potential energy in the spring when the kinetic energy of the mass was zero. In the next section we derive this result in a more general way.