Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Applying Newton's Laws of Motion
As a simple example, consider a mass  driven along a frictionless
surface by an ideal spring
driven along a frictionless
surface by an ideal spring 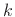 , as shown in Fig.B.2.
Assume that the mass position
, as shown in Fig.B.2.
Assume that the mass position 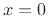 corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance
corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance  is given by Hooke's law (§B.1.3):
is given by Hooke's law (§B.1.3):
This force is balanced at all times by the inertial force
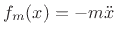 of
the mass
of
the mass  , i.e.
, i.e.  ,
yieldingB.6
,
yieldingB.6
 |
(B.4) |
where we have defined 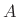 as the initial displacement of the mass
along
as the initial displacement of the mass
along  . This is a differential equation whose solution
gives the equation of motion of the mass-spring junction for all
time:B.7
. This is a differential equation whose solution
gives the equation of motion of the mass-spring junction for all
time:B.7
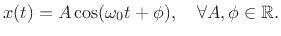 |
(B.5) |
where
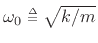 denotes the frequency of
oscillation in radians per second. More generally, the complete
space of solutions to Eq.(B.4), corresponding to all possible
initial displacements
denotes the frequency of
oscillation in radians per second. More generally, the complete
space of solutions to Eq.(B.4), corresponding to all possible
initial displacements 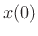 and initial velocities
and initial velocities
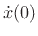 , is the
set of all sinusoidal oscillations at frequency
, is the
set of all sinusoidal oscillations at frequency  :
:
The amplitude of oscillation 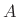 and phase offset
and phase offset 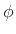 are
determined by the initial conditions, i.e., the initial position
are
determined by the initial conditions, i.e., the initial position
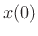 and initial velocity
and initial velocity
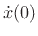 of the mass (its initial
state) when we ``let it go'' or ``push it off'' at time
of the mass (its initial
state) when we ``let it go'' or ``push it off'' at time 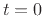 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]

![]() driven along a frictionless
surface by an ideal spring
driven along a frictionless
surface by an ideal spring ![]() , as shown in Fig.B.2.
Assume that the mass position
, as shown in Fig.B.2.
Assume that the mass position ![]() corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance
corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance ![]() is given by Hooke's law (§B.1.3):
is given by Hooke's law (§B.1.3):