Lowpass-Feedback Comb Filter

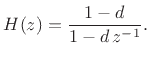
Inspection of comb.h in the Freeverb source shows that Freeverb's ``comb'' filter is more specifically a lowpass-feedback-comb filter (LBCF^4.11--§2.6.5). It is constructed using a delay line whose output is lowpass-filtered and summed with the delay-line's input. The particular lowpass used in Freeverb is a unity-gain one-pole lowpass having the transfer function

$$H(z) = \frac{1-d}{1-d\,z^{-1}}.$$

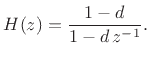
When $d=0$ , the LBCF reduces to the feedback comb filter (FBCF) of §2.6.2 in which the feedback was not filtered. The overall LBCF transfer function is then

$$\hbox{LBCF}_{N}^{\,f,\,d} \;\isdef \; \frac{z^{-N}}{1 - f\frac{1-d}{1-d\,z^{-1}}\,z^{-N}}.$$

This structure was introduced for artificial reverberation by Schroeder [415] and Moorer [317].

In Freeverb's comb section (comb.h and comb.cpp), the ``damping'' $d$ is set initially to

$$d = \texttt{damp = initialdamp * scaledamp} = 0.5 \cdot 0.4 = 0.2\; .$$

The lowpass scale-factor $f$ is called feedback in the source, and it is set initially to

$$\begin{eqnarray*} f &=& \texttt{roomsize = initialroom * scaleroom + offsetroom}\\ &=& 0.5 \cdot 0.28 + 0.7 = 0.84\;. \end{eqnarray*}$$

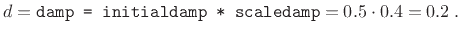
Increasing the roomsize parameter (typically brought out to a GUI slider) increases $f$ and hence the reverberation time. Since $f<1$ is required for dc stability, the roomsize must be less than 1.0714, and so the GUI slider max is typically 1 ($f=0.98$ ).

The feedback variable $f$ mainly determines reverberation time at low-frequencies at which the feedback lowpass has negligible effect. The feedback lowpass causes the reverberation time to decrease with frequency, which is natural. At very high frequencies--those for which the lowpass gain times $f$ is much less than 0.5--the reverberation time becomes dominated by the diffusion allpass filters (which have a fixed feedback coefficient of $g=0.5$ ). Thus, in Freeverb, the ``room size'' parameter can be interpreted as setting the low-frequency T60 (time to decay 60 dB), while the ``damping'' parameter controls how rapidly T60 shortens as a function of increasing frequency. A lower-limit on T60 is given by the four diffusion allpass filters.

In terms of the physical interpretation of the filtered-feedback comb-filter discussed in §2.6.5, Freeverb's roomsize parameter can be interpreted as the square-root of the low-frequency reflection-coefficient of each wall. That is, when a planewave bounces back and forth between two walls, the attenuation coefficient is roomsize after one round trip (two wall reflections). Therefore, a better name in this interpretation would be liveness or reflectivity. Since the round-trip delay is given in samples by the delay-line length, changing the roomsize requires changing the delay-line lengths in this interpretation.