Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
We will now derive a finite-difference model in terms of string
displacement samples which correspond to the lossy digital waveguide
model of Fig.C.5. This derivation generalizes the lossless case
considered in §C.4.3.
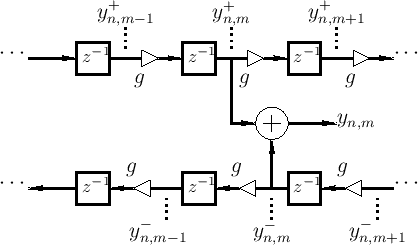
Figure C.7 depicts a digital waveguide section once again in
``physical canonical form,'' as shown earlier in Fig.C.5, and
introduces a doubly indexed notation for greater clarity in the
derivation below
[445,223,124,123].
Referring to Fig.C.7, we have the following time-update
relations:
Adding these equations gives
This is now in the form of the finite-difference time-domain (FDTD)
scheme analyzed in [223]:
with
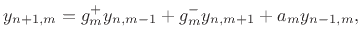 , and
, and 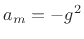 . In
[124], it was shown by von Neumann analysis
(§D.4) that these parameter choices give rise to a stable
finite-difference scheme (§D.2.3), provided
. In
[124], it was shown by von Neumann analysis
(§D.4) that these parameter choices give rise to a stable
finite-difference scheme (§D.2.3), provided  . In the
present context, we expect stability to follow naturally from starting
with a passive digital waveguide model.
. In the
present context, we expect stability to follow naturally from starting
with a passive digital waveguide model.
Subsections
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]