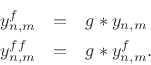Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The preceding derivation generalizes immediately to
frequency-dependent losses. First imagine each 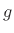 in Fig.C.7
to be replaced by
in Fig.C.7
to be replaced by 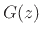 , where for passivity we require
, where for passivity we require
In the time domain, we interpret  as the impulse response
corresponding to
as the impulse response
corresponding to 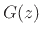 . We may now derive the frequency-dependent
counterpart of Eq.(C.31) as follows:
. We may now derive the frequency-dependent
counterpart of Eq.(C.31) as follows:
where  denotes convolution (in the time dimension only).
Define filtered node variables by
denotes convolution (in the time dimension only).
Define filtered node variables by
Then the frequency-dependent FDTD scheme is simply
We see that generalizing the FDTD scheme to frequency-dependent losses
requires a simple filtering of each node variable 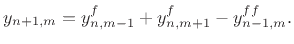 by the
per-sample propagation filter
by the
per-sample propagation filter 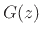 . For computational efficiency,
two spatial lines should be stored in memory at time
. For computational efficiency,
two spatial lines should be stored in memory at time  :
: 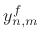 and
and
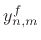 , for all
, for all  . These state variables enable computation of
. These state variables enable computation of
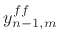 , after which each sample of
, after which each sample of 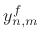 (
( ) is filtered
by
) is filtered
by 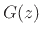 to produce
to produce
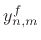 for the next iteration, and
for the next iteration, and 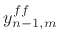 is filtered by
is filtered by 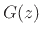 to produce
to produce 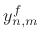 for the next iteration.
for the next iteration.
The frequency-dependent generalization of the FDTD scheme described in
this section extends readily to the digital waveguide mesh. See
§C.14.5 for the outline of the derivation.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() in Fig.C.7
to be replaced by
in Fig.C.7
to be replaced by ![]() , where for passivity we require
, where for passivity we require
![\begin{eqnarray*}
y^{+}_{n+1,m}&=& g\ast y^{+}_{n,m-1}\;=\; g\ast (y_{n,m-1}- y^{-}_{n,m-1})\\
y^{-}_{n+1,m}&=& g\ast y^{-}_{n,m+1}\;=\; g\ast (y_{n,m+1}- y^{+}_{n,m+1})\\ [10pt]
\Rightarrow\quad
y_{n+1,m}&=& g\ast (y_{n,m-1}+y_{n,m+1})
- g\ast (\underbrace{y^{-}_{n,m-1}}_{g\ast y^{-}_{n-1,m}} +
\underbrace{y^{+}_{n,m+1}}_{g\ast y^{+}_{n-1,m}})\nonumber \\
&=& g\ast (y_{n,m-1}+y_{n,m+1}) - g\ast g\ast y_{n-1,m}\\
&=& g\ast \left[(y_{n,m-1}+y_{n,m+1}) - g\ast y_{n-1,m}\right]
\end{eqnarray*}](img3377.png)
![]() denotes convolution (in the time dimension only).
Define filtered node variables by
denotes convolution (in the time dimension only).
Define filtered node variables by