| (C.28) |
In nearly all natural wave phenomena, losses increase with frequency. Distributed losses due to air drag and internal bulk losses in the string tend to increase monotonically with frequency. Similarly, air absorption increases with frequency, adding loss for sound waves in acoustic tubes or open air [321].
Perhaps the apparently simplest modification to Eq.(C.21) yielding frequency-dependent damping is to add a third-order time-derivative term [395]:
A well posed replacement for Eq.(C.28) is given by
The solution of a lossy wave equation containing higher odd-order
derivatives with respect to time yields traveling waves which
propagate with frequency-dependent attenuation. Instead of scalar
factors ![]() distributed throughout the diagram as in Fig.C.5,
each
distributed throughout the diagram as in Fig.C.5,
each ![]() factor becomes a lowpass filter having some
frequency-response per sample denoted by
factor becomes a lowpass filter having some
frequency-response per sample denoted by ![]() . Because
propagation is passive, we will always have
. Because
propagation is passive, we will always have
![]() .
.
More specically, As shown in [395], odd-order partial derivatives with respect to time in the wave equation of the form
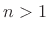
correspond to attenuation of traveling waves on the string. (The even-order time derivatives can be associated with variations in dispersion as a function of frequency, which is considered in §C.6 below.) For

In particular, if the wave equation (C.21) is modified by adding terms proportional to
where the
In view of the above, we see that we can add odd-order time derivatives to the wave equation to approximate experimentally observed frequency-dependent damping characteristics in vibrating strings [73]. However, we then have the problem that such wave equations are ill posed, leading to possible stability failures at high sampling rates. As a result, it is generally preferable to use mixed derivatives, as in Eq.(C.29), and try to achieve realistic damping using higher order spatial derivatives instead.