Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
For completeness, this section derives the Householder reflection
matrix from geometric considerations [454]. Let
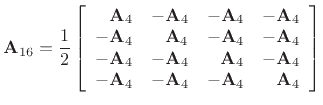 denote
the projection matrix which orthogonally projects vectors onto
denote
the projection matrix which orthogonally projects vectors onto
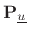 , i.e.,
, i.e.,
and
specifically projects
 onto
onto
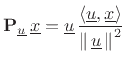 . Since the projection
is orthogonal, we have
. Since the projection
is orthogonal, we have
We may interpret
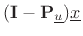 as the difference vector between
as the difference vector between
 and
and
 , its orthogonal projection onto
, its orthogonal projection onto
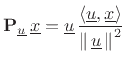 , since
, since
and we have
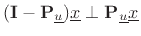 by definition of the orthogonal
projection. Consequently, the projection onto
by definition of the orthogonal
projection. Consequently, the projection onto
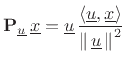 minus this
difference vector gives a reflection of the vector
minus this
difference vector gives a reflection of the vector
 about
about
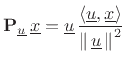 :
:
Thus,
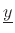 is obtained by reflecting
is obtained by reflecting
 about
about
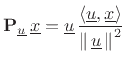 --a so-called
Householder reflection.
--a so-called
Householder reflection.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() denote
the projection matrix which orthogonally projects vectors onto
denote
the projection matrix which orthogonally projects vectors onto
![]() , i.e.,
, i.e.,