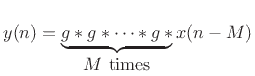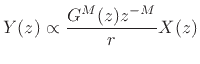Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Frequency-Dependent Air-Absorption
Filtering
More generally, frequency-dependent air
absorption can be modeled using the substitution
where 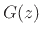 denotes the filtering per sample in the
propagation medium. Since air absorption cannot amplify a wave at any
frequency, we have
denotes the filtering per sample in the
propagation medium. Since air absorption cannot amplify a wave at any
frequency, we have
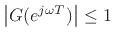 . A lossy delay line for
plane-wave simulation is thus described by
. A lossy delay line for
plane-wave simulation is thus described by
in the frequency domain, and
in the time domain, where ` ' denotes convolution, and
' denotes convolution, and  is
the impulse response of the per-sample loss filter
is
the impulse response of the per-sample loss filter 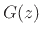 . The effect
of
. The effect
of 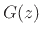 on the poles of the system is discussed in §3.7.4.
on the poles of the system is discussed in §3.7.4.
For spherical waves, the loss due to spherical spreading is of the form
where 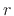 is the distance from
is the distance from  to
to 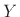 . We see that the spherical
spreading loss factor is ``hyperbolic'' in the propagation distance
. We see that the spherical
spreading loss factor is ``hyperbolic'' in the propagation distance
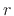 , while air absorption is exponential in
, while air absorption is exponential in 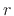 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]