First-Order Delay-Filter Design

The first-order case is very simple while enabling separate control of low-frequency and high-frequency reverberation times. For simplicity, let's specify $t_{60}(0)$ and $t_{60}(\pi/T)$ , denoting the desired decay-time at dc ($\omega=0$ ) and half the sampling rate ( $\omega=\pi/T$ ). Then we have determined the coefficients of a one-pole filter:

$$H_i(z) = \frac{g_i}{1-p_iz^{-1}}$$

The dc gain of this filter is $H_i(1)=g_i/(1-p_i)$ , while the gain at $\omega=\pi/T$ is $H_i(-1)=g_i/(1+p_i)$ . From Eq.(3.9) (or Eq.(3.8)), we obtain two equations in two unknowns:

$$\begin{eqnarray*} \frac{g_i}{1-p_i} &=& 10^{-3 M_i T / t_{60}(0)} \eqsp e^{-M_iT/\tau(0)} \isdefs R_0^{M_i}\\ [5pt] \frac{g_i}{1+p_i} &=& 10^{-3 M_i T / t_{60}(\pi/T)} \eqsp e^{-M_iT/\tau(\pi/T)} \isdefs R_\pi^{M_i}\\ [5pt] \end{eqnarray*}$$

where $D_i\isdeftext M_iT$ denotes the $i$ th delay-line length in seconds. These two equations are readily solved to yield

$$\begin{eqnarray*} p_i &=& \frac{R_0^{M_i}-R_\pi^{M_i}}{R_0^{M_i}+R_\pi^{M_i}}\\ [5pt] g_i &=& \frac{2R_0^{M_i}R_\pi^{M_i}}{R_0^{M_i}+R_\pi^{M_i}} \end{eqnarray*}$$

The truncated series approximation

$$R_\omega^{M_i} \isdefs e^{-\frac{M_iT}{\tau(\omega)}} \approxs 1 - \frac{M_iT}{\tau(\omega)} \approxs 1 - \frac{6.91\,M_iT}{t_{60}(\omega)} \isdefs 1 - \frac{6.91\,M_i}{n_{60}(\omega)}$$

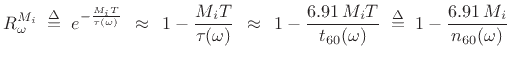
has been found to work well in practical FDN reverberators.