e^(j theta)

We've now defined $a^z$ for any positive real number $a$ and any complex number $z$ . Setting $a=e$ and $z=j\theta$ gives us the special case we need for Euler's identity. Since $e^x$ is its own derivative, the Taylor series expansion for $f(x)=e^x$ is one of the simplest imaginable infinite series:

$$e^x = \sum_{n=0}^\infty \frac{x^n}{n!} = 1 + x + \frac{x^2}{2} + \frac{x^3}{3!} + \cdots$$

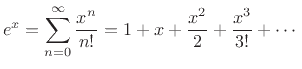
The simplicity comes about because $f^{(n)}(0)=1$ for all $n$ and because we chose to expand about the point $x=0$ . We of course define

$$e^{j\theta} \isdef \sum_{n=0}^\infty \frac{(j\theta)^n}{n!} = 1 + j\theta - \frac{\theta^2}{2} - j\frac{\theta^3}{3!} + \cdots \,.$$

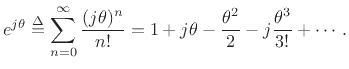
Note that all even-order terms are real while all odd-order terms are imaginary. Separating out the real and imaginary parts gives

$$\begin{eqnarray*} \mbox{re}\left\{e^{j\theta}\right\} &=& 1 - \theta^2/2 + \theta^4/4! - \cdots \\ [5pt] \mbox{im}\left\{e^{j\theta}\right\} &=& \theta - \theta^3/3! + \theta^5/5! - \cdots\,. \end{eqnarray*}$$

Comparing the Maclaurin expansion for $e^{j\theta }$ with that of $\cos(\theta)$ and $\sin(\theta)$ proves Euler's identity. Recall from introductory calculus that

$$\begin{eqnarray*} \frac{d}{d\theta}\cos(\theta) &=& -\sin(\theta) \\ [5pt] \frac{d}{d\theta}\sin(\theta) &=& \cos(\theta) \end{eqnarray*}$$

so that

$$\begin{eqnarray*} \left.\frac{d^n}{d\theta^n}\cos(\theta)\right\vert _{\theta=0} &=& \left\{\begin{array}{ll} (-1)^{n/2}, & n\;\mbox{\small even} \\ [5pt] 0, & n\;\mbox{\small odd} \\ \end{array} \right. \\ [10pt] \left.\frac{d^n}{d\theta^n}\sin(\theta)\right\vert _{\theta=0} &=& \left\{\begin{array}{ll} (-1)^{(n-1)/2}, & n\;\mbox{\small odd} \\ [5pt] 0, & n\;\mbox{\small even}. \\ \end{array} \right. \end{eqnarray*}$$

Plugging into the general Maclaurin series gives

$$\begin{eqnarray*} \cos(\theta) &=& \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}\theta^n \\ &=& \sum_{\stackrel{n\geq 0}{\vspace{2pt}\mbox{\tiny$n$\ even}}}^\infty \frac{(-1)^{n/2}}{n!} \theta^n \\ \sin(\theta) &=& \sum_{\stackrel{n\geq 0}{\vspace{2pt}\mbox{\tiny$n$\ odd}}}^\infty \frac{(-1)^{(n-1)/2}}{n!} \theta^n. \end{eqnarray*}$$

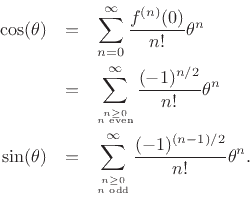
Separating the Maclaurin expansion for $e^{j\theta }$ into its even and odd terms (real and imaginary parts) gives

$$\begin{eqnarray*} e^{j\theta} \isdef \sum_{n=0}^\infty \frac{(j\theta)^n}{n!} &=& \sum_{\stackrel{n\geq 0}{\vspace{2pt}\mbox{\tiny$n$\ even}}}^\infty \frac{(-1)^{n/2}}{n!} \theta^n + j \sum_{\stackrel{n\geq 0}{\vspace{2pt}\mbox{\tiny$n$\ odd}}}^\infty \frac{(-1)^{(n-1)/2}}{n!} \theta^n\\ &=& \cos(\theta) + j\sin(\theta) \end{eqnarray*}$$

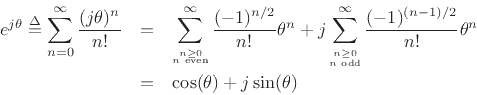
thus proving Euler's identity.