Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Back to Mth Roots
As mentioned in §3.4, there are 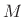 different numbers
different numbers 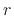 which satisfy
which satisfy 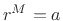 when
when 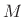 is a positive integer.
That is, the
is a positive integer.
That is, the 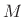 th root of
th root of 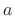 , which is
written as
, which is
written as 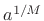 , is not unique--there are
, is not unique--there are 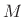 of them. How do
we find them all? The answer is to consider complex numbers in
polar form.
By Euler's Identity, which we just proved, any number,
real or complex, can be written in polar form as
of them. How do
we find them all? The answer is to consider complex numbers in
polar form.
By Euler's Identity, which we just proved, any number,
real or complex, can be written in polar form as
where 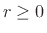 and
and
 are real numbers.
Since, by Euler's identity,
are real numbers.
Since, by Euler's identity,
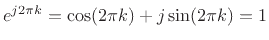 for every integer
for every integer 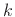 , we also have
, we also have
Taking the 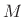 th root gives
th root gives
There are 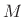 different results obtainable using different values of
different results obtainable using different values of
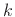 , e.g.,
, e.g.,
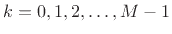 . When
. When 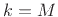 , we get the same thing as
when
, we get the same thing as
when 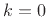 . When
. When 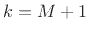 , we get the same thing as when
, we get the same thing as when 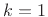 , and so
on, so there are only
, and so
on, so there are only 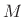 distinct cases. Thus, we may define the
distinct cases. Thus, we may define the
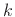 th
th 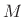 th-root of
th-root of
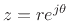 as
as
These are the 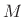
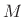 th-roots of the complex number
th-roots of the complex number
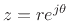 .
.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() different numbers
different numbers ![]() which satisfy
which satisfy ![]() when
when ![]() is a positive integer.
That is, the
is a positive integer.
That is, the ![]() th root of
th root of ![]() , which is
written as
, which is
written as ![]() , is not unique--there are
, is not unique--there are ![]() of them. How do
we find them all? The answer is to consider complex numbers in
polar form.
By Euler's Identity, which we just proved, any number,
real or complex, can be written in polar form as
of them. How do
we find them all? The answer is to consider complex numbers in
polar form.
By Euler's Identity, which we just proved, any number,
real or complex, can be written in polar form as