Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Above, we defined 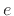 as the particular real number satisfying
as the particular real number satisfying
which gave us
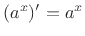 when
when 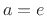 . From this expression,
we have, as
. From this expression,
we have, as
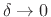 ,
,
or
This is one way to define 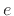 . Another way to arrive at the same
definition is to ask what logarithmic base
. Another way to arrive at the same
definition is to ask what logarithmic base 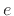 gives that the derivative of
gives that the derivative of
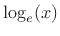 is
is 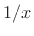 . We denote
. We denote 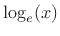 by
by  .
.
Numerically, 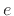 is a transcendental number (a type of irrational
number3.5), so its decimal expansion never repeats.
The initial decimal expansion of
is a transcendental number (a type of irrational
number3.5), so its decimal expansion never repeats.
The initial decimal expansion of 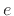 is given by3.6
is given by3.6
Any number of digits can be computed from the formula
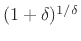 by making
by making 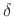 sufficiently small.
sufficiently small.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() as the particular real number satisfying
as the particular real number satisfying
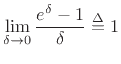
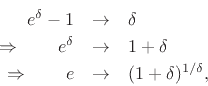
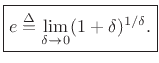
![]() is a transcendental number (a type of irrational
number3.5), so its decimal expansion never repeats.
The initial decimal expansion of
is a transcendental number (a type of irrational
number3.5), so its decimal expansion never repeats.
The initial decimal expansion of ![]() is given by3.6
is given by3.6