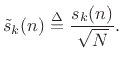
Note that the power theorem would be more elegant if the DFT were defined as the coefficient of projection onto the normalized DFT sinusoids
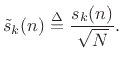
That is, for the normalized DFT (§6.10), the power theorem becomes simply
We see that the power theorem expresses the invariance of the inner product between two signals in the time and frequency domains. If we think of the inner product geometrically, as in Chapter 5, then this result is expected, because