Theorem: For all
Theorem: For all
![]() ,
,
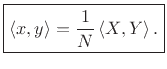
Proof:
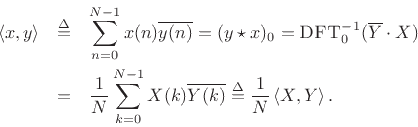
As mentioned in §5.8, physical power is
energy per unit time.7.20 For example, when a force produces a motion,
the power delivered is given by the force times the
velocity of the motion. Therefore, if ![]() and
and ![]() are in
physical units of force and velocity (or any analogous quantities such
as voltage and current, etc.), then their product
are in
physical units of force and velocity (or any analogous quantities such
as voltage and current, etc.), then their product
![]() is proportional to the power per sample at time
is proportional to the power per sample at time ![]() ,
and
,
and
![]() becomes proportional to the total energy
supplied (or absorbed) by the driving force. By the power theorem,
becomes proportional to the total energy
supplied (or absorbed) by the driving force. By the power theorem,
![]() can be interpreted as the energy per bin in
the DFT, or spectral power, i.e., the energy associated with a
spectral band of width
can be interpreted as the energy per bin in
the DFT, or spectral power, i.e., the energy associated with a
spectral band of width ![]() .7.21
.7.21