Orthogonality of the DFT Sinusoids

We now show mathematically that the DFT sinusoids are exactly orthogonal. Let

$$s_k(n) \isdef e^{j\omega_k nT} = e^{j2\pi k n /N} = \left[W_N^k\right]^n, \quad n=0,1,2,\ldots,N-1,$$

denote the $k$th DFT complex-sinusoid, for $k=0:N-1$. Then

$$\begin{eqnarray*} \left<s_k,s_l\right> &\isdef & \sum_{n=0}^{N-1}s_k(n) \overlin... ...i (k-l) n /N} = \frac{1 - e^{j2\pi (k-l)}}{1-e^{j2\pi (k-l)/N}} \end{eqnarray*}$$

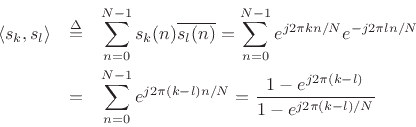
where the last step made use of the closed-form expression for the sum of a geometric series (§6.1). If $k\neq l$, the denominator is nonzero while the numerator is zero. This proves

$$\zbox {s_k \perp s_l, \quad k \neq l.}$$

While we only looked at unit amplitude, zero-phase complex sinusoids, as used by the DFT, it is readily verified that the (nonzero) amplitude and phase have no effect on orthogonality.