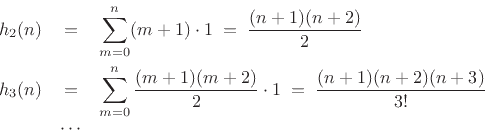In the previous section, we found that repeated poles give rise to polynomial amplitude-envelopes multiplying the exponential decay due to the pole. On the other hand, two different poles can only yield a convolution (or sum) of two different exponential decays, with no polynomial envelope allowed. This is true no matter how closely the poles come together; the polynomial envelope can occur only when the poles merge exactly. This might violate one's intuitive expectation of a continuous change when passing from two closely spaced poles to a repeated pole.
To study this phenomenon further, consider the convolution of two
one-pole impulse-responses
![]() and
and
![]() :
:
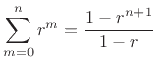
Applying this to Eq.(6.14) yields
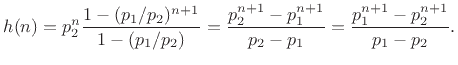
Note that the result is symmetric in
Going back to Eq.(6.14), we have
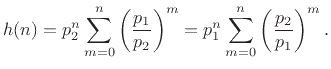 |
(7.15) |
| (7.16) |
We also see that the polynomial amplitude-envelopes fundamentally
arise from iterated convolutions. This corresponds to the
repeated poles being arranged in series, rather than in
parallel. The simplest case is when the repeated pole is at ![]() , in
which case its impulse response is a constant:
, in
which case its impulse response is a constant:
![$\displaystyle \frac{1}{1-z^{-1}} \eqsp
1 + z^{-1}+ z^{-2}+ \cdots \;\longleftrightarrow\; [1,1,1,\ldots]
$](img795.png)
The convolution of a constant with itself is a ramp:
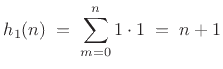
The convolution of a constant and a ramp is a quadratic, and so on:7.10