The z transform of a finite-amplitude
signal ![]() will always exist provided (1) the signal starts at a finite time and (2) it is
asymptotically exponentially bounded, i.e., there exists a
finite integer
will always exist provided (1) the signal starts at a finite time and (2) it is
asymptotically exponentially bounded, i.e., there exists a
finite integer ![]() , and finite real numbers
, and finite real numbers ![]() and
and ![]() ,
such that
,
such that
![]() for all
for all ![]() . The
bounding exponential may even be growing with
. The
bounding exponential may even be growing with ![]() (
(![]() ). These are
not the most general conditions for existence of the z transform, but they
suffice for most practical purposes.
). These are
not the most general conditions for existence of the z transform, but they
suffice for most practical purposes.
For a signal ![]() growing as
growing as
![]() , for
, for ![]() , one
would naturally expect the z transform
, one
would naturally expect the z transform ![]() to be defined only in the
region
to be defined only in the
region
![]() of the complex plane. This is expected
because the infinite series
of the complex plane. This is expected
because the infinite series
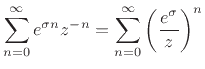
requires
More generally, it turns out that, in all cases of practical interest,
the domain of ![]() can be extended to include the
entire complex plane, except at isolated ``singular''
points7.2 at which
can be extended to include the
entire complex plane, except at isolated ``singular''
points7.2 at which ![]() approaches
infinity (such as at
approaches
infinity (such as at
![]() when
when
![]() ).
The mathematical technique for doing this is called analytic
continuation, and it is described in §D.1 as applied to the
Laplace transform (the continuous-time counterpart of the z transform).
A point to note, however, is that in the extension region (all points
).
The mathematical technique for doing this is called analytic
continuation, and it is described in §D.1 as applied to the
Laplace transform (the continuous-time counterpart of the z transform).
A point to note, however, is that in the extension region (all points
![]() such that
such that
![]() in the above example), the signal
component corresponding to each singularity inside the extension
region is ``flipped'' in the time domain. That is, ``causal''
exponentials become ``anticausal'' exponentials, as discussed in
§8.7.
in the above example), the signal
component corresponding to each singularity inside the extension
region is ``flipped'' in the time domain. That is, ``causal''
exponentials become ``anticausal'' exponentials, as discussed in
§8.7.
The z transform is discussed more fully elsewhere [52,60], and we will derive below only what we will need.