The bilateral z transform of the discrete-time signal ![]() is
defined to be
is
defined to be
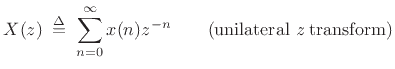 |
(7.2) |
Recall (§4.1) that the mathematical representation of a
discrete-time signal ![]() maps each integer
maps each integer
![]() to a complex
number (
to a complex
number (
![]() ) or real number (
) or real number (
![]() ). The z transform
of
). The z transform
of ![]() , on the other hand,
, on the other hand, ![]() , maps every complex number
, maps every complex number
![]() to a new complex number
to a new complex number
![]() . On a higher
level, the z transform, viewed as a linear operator, maps an entire
signal
. On a higher
level, the z transform, viewed as a linear operator, maps an entire
signal ![]() to its z transform
to its z transform ![]() . We think of this as a ``function to
function'' mapping. We may say
. We think of this as a ``function to
function'' mapping. We may say ![]() is the z transform of
is the z transform of ![]() by writing
by writing
or, using operator notation,
which can be abbreviated as
One also sees the convenient but possibly misleading notation
The z transform of a signal ![]() can be regarded as a polynomial in
can be regarded as a polynomial in
![]() , with coefficients given by the signal samples. For example,
the signal
, with coefficients given by the signal samples. For example,
the signal
![$\displaystyle x(n) = \left\{\begin{array}{ll}
n+1, & 0\leq n \leq 2 \\ [5pt]
0, & \mbox{otherwise} \\
\end{array} \right.
$](img629.png)
has the z transform