Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Digital filters can be expressed in state-space form as
by simply enumerating all delay elements as state variables
![$ \underline{x}^T(n)
= [x_1(n), x_2(n),\ldots, x_N(n)]$](img101.png) , and finding the state transition
matrix
, and finding the state transition
matrix 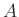 by inspection. Any inputs are collected in
by inspection. Any inputs are collected in
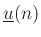 and
determine the
and
determine the 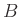 matrix.
matrix.
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download WaveDigitalFilters.pdf
Download WaveDigitalFilters_2up.pdf
Download WaveDigitalFilters_4up.pdf