Spectrum Warping

This method uses the fact that we can use the bilinear transform to map the unit circle onto itself warped. In particular, we can map $z=1$ to $\tilde{z}=1$ , $z=-1$ to $\tilde{z}=-1$ , and have one more degree of freedom left. Such a map is

$$z^{-1} \leftarrow \frac{z^{-1} - \beta}{1 - \beta z^{-1}}$$

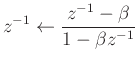
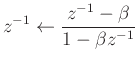
which, when the delays in a filter are replaced by the given allpass filter, preserves the magnitude response, but warps the frequency axis according to $\beta$ .

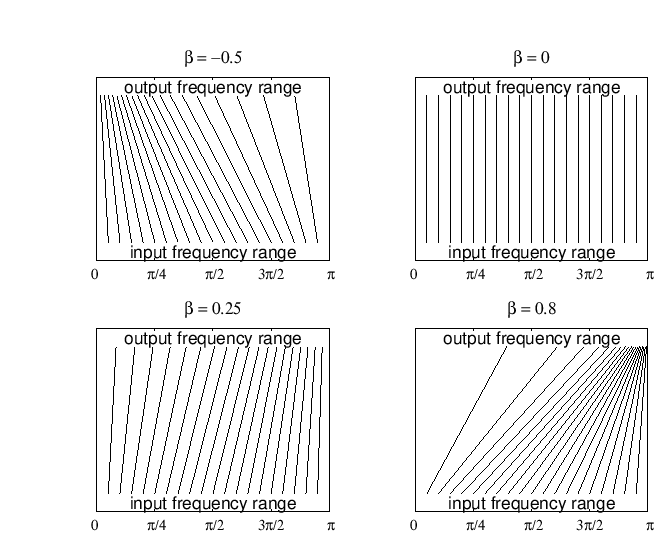
Thus a prototype filter (low-pass, for example) can be warped to place its corner frequency anywhere in the frequency range, so that $\beta$ becomes a simple and efficient tuning sweep control.

This method has a problem when applied to IIR prototype filters: the allpass filter has a delay-free path, which makes the feedback paths of the IIR filter unimplementable. Various methods exist to fix this problem, involving placing a delay in the loop, and fixing up the feedback coefficients. Unfortunately, all of these methods require that the fixed-up coefs be recomputed each time $\beta$ is changed, though some are much more efficient that others.

Another spectrum warping method, which preserves linear-phase in FIR filters, was proposed in ``Variable Cutoff Linear Phase Digital Filters'', Oppenhein, Mecklenbräuker, & Mersereau, IEEE Trans. Circuits and Systems, v23 n4, April 1976.