Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Pressure Plane Waves:
where
 are
are
Longitudinal Particle-Velocity Waves
Ohm's Law for Traveling Acoustic Plane Waves:
where
is the wave impedance of air in terms of mass density 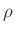 (
kg
(
kg m
m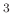 ) and sound speed
) and sound speed 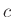 .
.
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download StringWaves.pdf
Download StringWaves_2up.pdf
Download StringWaves_4up.pdf


![]() are
are
![\fbox{%
\begin{minipage}[c]{3in}%
\begin{displaymath}\begin{array}{rcrl}%
p^+(n)&=&& R_au^{+}(n) \\
p^-(n)&=&-& R_au^{-}(n)
\end{array}\end{displaymath}\end{minipage}}](img72.png)