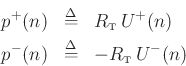
In acoustic tubes, we again work with
Pressure Plane Waves:
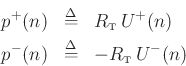
However, now
![]() are
are
Longitudinal Volume-Velocity Waves:
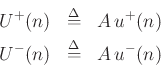
where ![]() is the cross-sectional area of the tube. In an acoustic
tube, it is volume velocity that is conserved from one tube section to
the next.
is the cross-sectional area of the tube. In an acoustic
tube, it is volume velocity that is conserved from one tube section to
the next.
Ohm's Law for Traveling Plane Waves in an Acoustic Tube:
![\fbox{%
\begin{minipage}[c]{3in}%
\begin{displaymath}\begin{array}{rcrl}%
p^+(n)&=&&R_{\hbox{\tiny T}}\,U^{+}(n) \\
p^-(n)&=&-&R_{\hbox{\tiny T}}\,U^{-}(n)
\end{array}\end{displaymath}\end{minipage}}](img81.png)

is the wave impedance of air in terms of mass density