Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Transverse Velocity Waves:
Wave Impedance (we'll derive later):
Force Waves:
Ohm's Law for Traveling Waves:
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download StringWaves.pdf
Download StringWaves_2up.pdf
Download StringWaves_4up.pdf
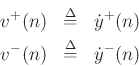
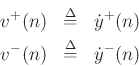
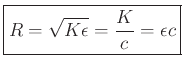

![\fbox{%
\begin{minipage}[c]{3in}%
\begin{displaymath}\begin{array}{rcrl}%
f^{{+}}(n)&=&&R\,v^{+}(n) \\
f^{{-}}(n)&=&-&R\,v^{-}(n)
\end{array}\end{displaymath}\end{minipage}}](img69.png)