Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The damping filter 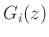 associated with the delay line
of length
associated with the delay line
of length 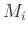 in the FDN can be written in principle as
in the FDN can be written in principle as
where  is the lowpass filter corresponding to one
sample of wave propagation through air, and
is the lowpass filter corresponding to one
sample of wave propagation through air, and 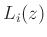 is a lowpass
corresponding to absorbing/scattering boundary reflections along the
(hypothetical)
is a lowpass
corresponding to absorbing/scattering boundary reflections along the
(hypothetical) 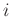 th propagation path.
th propagation path.
Define
We can introduce frequency-independent damping with the (conformal map)
substitution
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Reverb.pdf
Download Reverb_2up.pdf
Download Reverb_4up.pdf
![]() associated with the delay line
of length
associated with the delay line
of length ![]() in the FDN can be written in principle as
in the FDN can be written in principle as
![\begin{eqnarray*}
t_{60}(\omega)&=& \mbox{desired reverberation time at frequency $\omega$}\\ [10pt]
p_k &=& e^{j\omega_kT} = \mbox{$k$th pole of the lossless prototype}
\end{eqnarray*}](img100.png)