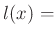 inductance/unit length
inductance/unit length
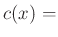 shunt capacitance/unit length
shunt capacitance/unit length
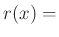 resistance/unit length
resistance/unit length
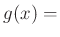 shunt conductance/unit length
shunt conductance/unit length
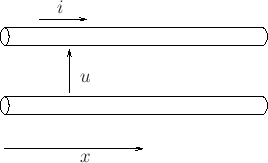
The 1D Transmission Line

The 1D Transmission Line (cont'd)
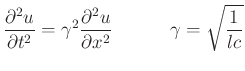 |
Otherwise, describes dispersive, lossy 1D wave propagation.
First Attempt at a Kirchoff Circuit (cont'd)
We can write the telegrapher's equations down directly as a two-loop circuit, with currents ![]() and
and
![]()
![]() scaling parameter, dimensions of resistance:
scaling parameter, dimensions of resistance:
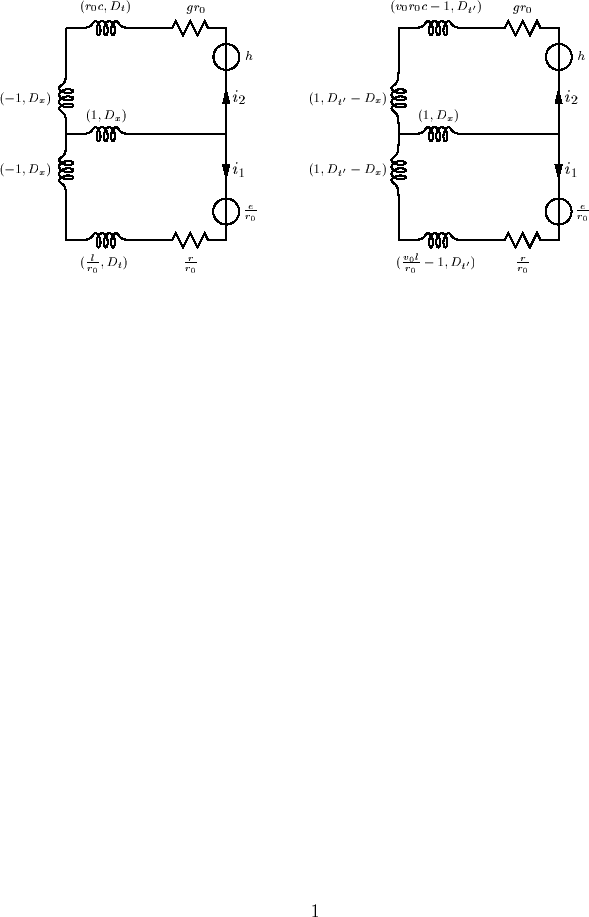
Problem: Not MD-passive.
Fix: Classical network theory manipulations.
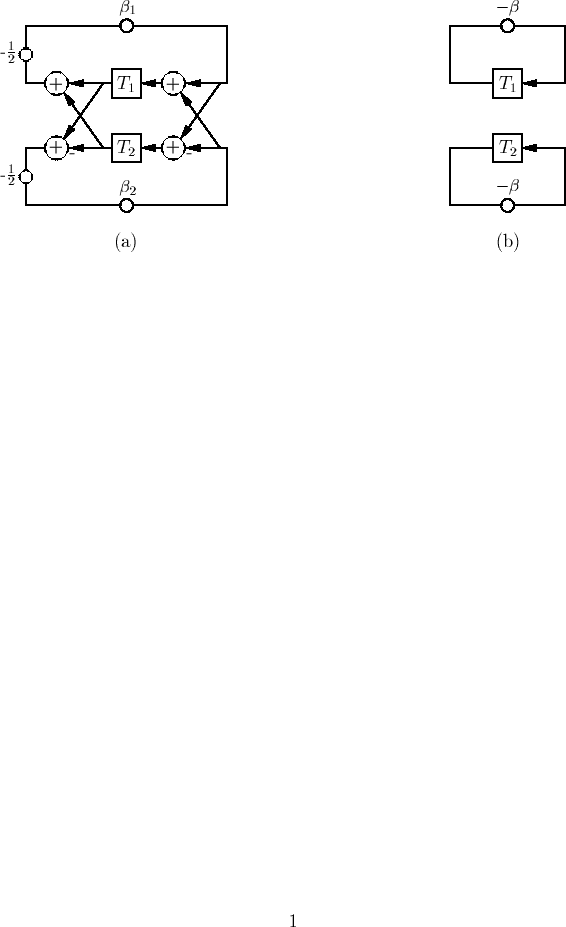
Passive MD Circuit
To any T-junction corresponds a lattice or Jaumann equivalent:

Employing this equivalence gives a concretely MD-passive structure
Comments
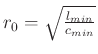 , the stability bound is
, the stability bound is
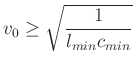 |
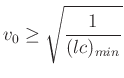 |
Simplifications
If ![]() and
and ![]() are constant, and we have no sources then we can derive a simplified form (a).
are constant, and we have no sources then we can derive a simplified form (a).
If in addition, we have ![]() , then the line is distorionless, and we have simple travelling waves, which are attenuated (b).
, then the line is distorionless, and we have simple travelling waves, which are attenuated (b).
2D ``Parallel Plate''
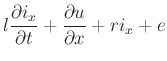 |
0 | ||
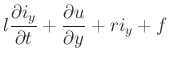 |
0 | ||
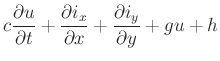 |
0 |
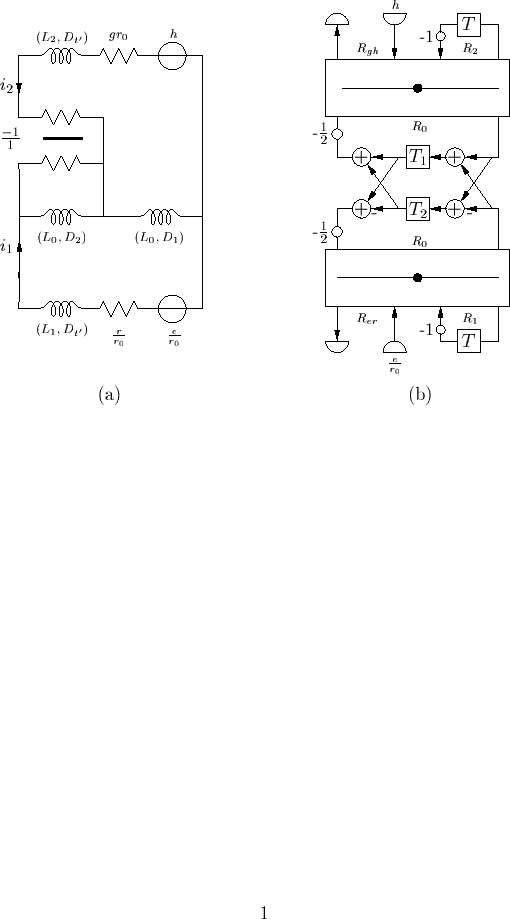
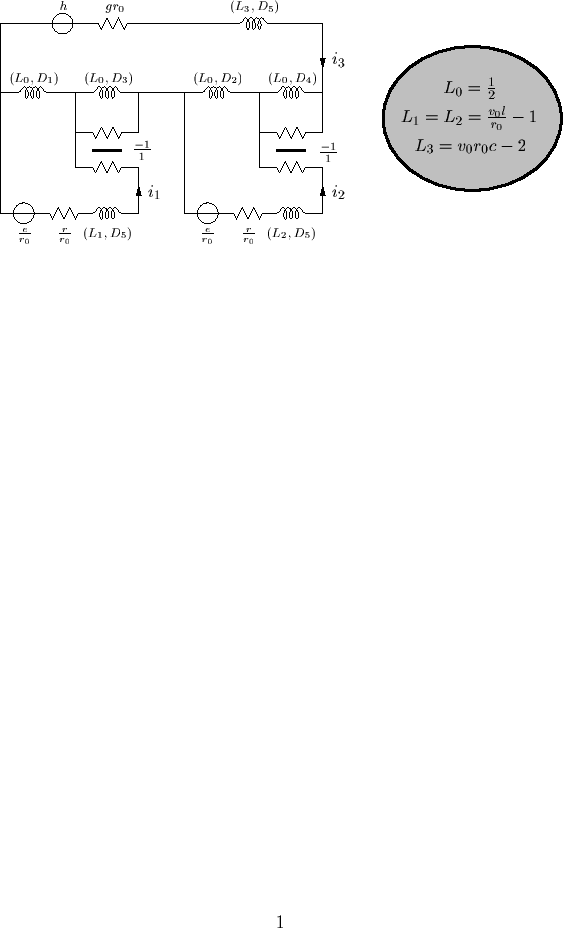
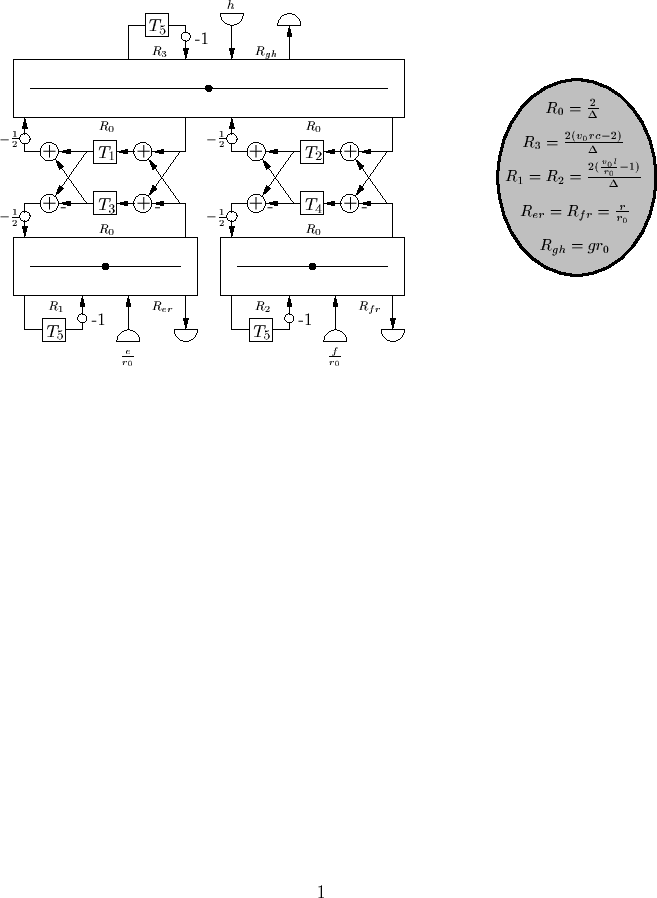
A Passive Circuit and Wave Digital Network
Applying a coordinate transformation (for rectangular coordinates), we get the following circuit and network:
Other Systems
The circuit approach is applicable to a wide range of problems including:
and with some tampering, to parabolic/borderline parabolic problems like
Most interestingly, the method can also be applied to systems of nonlinear conservation laws, in particular