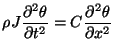Longitudinal and Torsional Waves in Rods

In addition to transverse waves, a one-dimensional stiff medium can support longitudinal and torsional waves [66,77]. In these cases, the medium is usually referred to as a rod or bar instead of a beam [83,146].

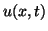When a bar aligned with the $x$-axis is vibrating longitudinally, motion within the medium will only occur in the $x$ direction. If $u(x,t)$ represents the longitudinal displacement of the medium at position $x$ and time 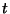$t$, the equation of motion of the bar [146] is

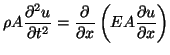$$\rho A \frac{\partial^{2} u}{\partial t^{2}} = \frac{\partial}{\partial x}\left(EA\frac{\partial u}{\partial x}\right)$$ (5.30)

which is easily identified the second-order equation describing the behavior of current or voltage in the (1+1)D transmission line, as per (4.39). Thus all methods applicable to the (1+1)D transmission line discussed in this work are applicable to this case as well. Note that in the case of constant material parameters and cross-sectional area, (5.29) becomes the (1+1)D wave equation, and thus longitudinal waves travel non-dispersively (in contrast to transverse waves). Here, lateral inertia effects have been neglected--that is, even though the medium undergoes axial compression and expansion, the bar is not allowed to compensate for this by becoming ``fatter'' or ``thinner'' respectively. The so-called Love theory [77] is an attempt to account for this important effect; it should be possible to apply scattering-based numerical methods to the Love theory, although we have not attempted to do so.

Torsional motion involves the propagation of a twisting disturbance along the length of the bar. For a bar of constant cross-section, the equation of motion here is

$$\rho J \frac{\partial^{2}\theta}{\partial t^{2}} = C\frac{\partial^{2}\theta}{\partial x^{2}}$$

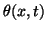where $\theta(x,t)$ is the angle at which the bar is twisted relative to its equilibrium state, 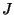$J$ is the polar moment of inertia, and 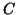$C$ is a constant which depends on the geometry of the cross section [77]. Here again, we have the basic (1+1)D transmission line form, and the comments made regarding longitudinal waves apply equally well here.