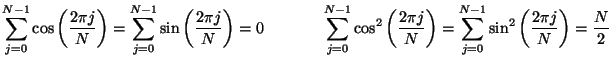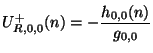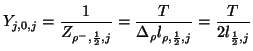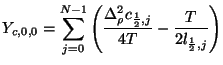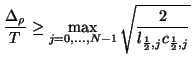Next: Simulation: Circular Region with
Up: The Waveguide Mesh in
Previous: Type II: Current-Centered Mesh
We have so far restricted our attention to interior points of the grid (for which  ). If the center of the
). If the center of the
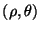 coordinate system is to be contained in the grid, a special treatment is required. We have indexed the grid variables such that, in our interleaved mesh, a single parallel junction lies at the origin (for
coordinate system is to be contained in the grid, a special treatment is required. We have indexed the grid variables such that, in our interleaved mesh, a single parallel junction lies at the origin (for 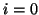 ). If the problem domain includes a full circle, we also must assume that
). If the problem domain includes a full circle, we also must assume that
 divides 2
divides 2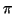 evenly so that we have a positive integer
evenly so that we have a positive integer  such that
such that
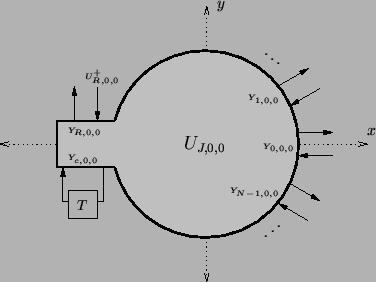
Thus the central parallel junction will be connected to  series junctions at locations
series junctions at locations
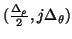 ,
,
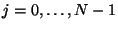 . We will name the admittances of the
. We will name the admittances of the  waveguides radiating from the central hub
waveguides radiating from the central hub 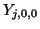 ,
,
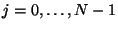 , and the admittance of the self-loop and loss/source ports will be
, and the admittance of the self-loop and loss/source ports will be  and
and 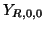 respectively (see Figure 4.31).
respectively (see Figure 4.31).
Figure 4.31:
Central scattering junction for the waveguide mesh in radial coordinates.
 |
The difference scheme relating the junction voltage at the central grid point to the radial currents at the surrounding junctions will then be
The sum over the junction currents, which we now look at in the continuous time/space domain so as to develop a series approximation) may be rewritten using (4.83) in terms of the rectilinear current variables as
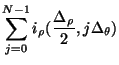 |
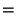 |
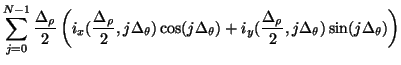 |
(4.107) |
| |
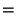 |
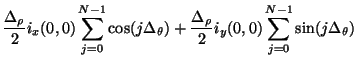 |
(4.108) |
| |
|
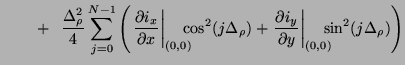 |
(4.109) |
| |
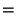 |
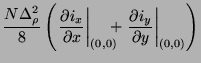 |
(4.110) |
where we have neglected higher order terms in
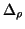 and used, in the last line, the identities
and used, in the last line, the identities
which hold for  . Using approximation (4.94) and by comparing (4.93) with (4.82c), we must choose the junction and loss/source port admittance to be
. Using approximation (4.94) and by comparing (4.93) with (4.82c), we must choose the junction and loss/source port admittance to be
and the source wave variable
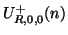 to be
to be
A mesh of type I is infeasible because it would require access to
 in order to set
in order to set
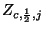 as prescribed in (4.86), but
as prescribed in (4.86), but 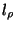 as defined in (4.84) is singular at the origin (although if we are working with a radial geometry which does not contain the origin, this problem does not arise). For a mesh of type II, we have, from (4.89),
as defined in (4.84) is singular at the origin (although if we are working with a radial geometry which does not contain the origin, this problem does not arise). For a mesh of type II, we have, from (4.89),
and so we may set, for the self-loop admittance at the central junction,
which is positive when
Thus the stability requirement at the central junction does not interfere with the requirements over the interior of the mesh given for the type II mesh.
We note that a different type of central node, proposed for use in radial TLM simulations, is described in [24].



Next: Simulation: Circular Region with
Up: The Waveguide Mesh in
Previous: Type II: Current-Centered Mesh
Stefan Bilbao
2002-01-22
![]() ). If the center of the
). If the center of the
![]() coordinate system is to be contained in the grid, a special treatment is required. We have indexed the grid variables such that, in our interleaved mesh, a single parallel junction lies at the origin (for
coordinate system is to be contained in the grid, a special treatment is required. We have indexed the grid variables such that, in our interleaved mesh, a single parallel junction lies at the origin (for ![]() ). If the problem domain includes a full circle, we also must assume that
). If the problem domain includes a full circle, we also must assume that
![]() divides 2
divides 2![]() evenly so that we have a positive integer
evenly so that we have a positive integer ![]() such that
such that