Next: Type II: Current-Centered Mesh
Up: The Waveguide Mesh in
Previous: The Waveguide Mesh in
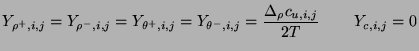 |
(4.97) |
The stability constraints (which follow from the requirement of positivity of 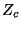 everywhere) are
everywhere) are
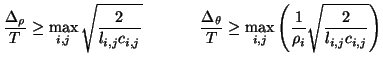 |
(4.100) |
There is thus a dependence on 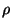 in the second condition (relating the angular spacing
in the second condition (relating the angular spacing
 to
to 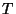 ), which we expect, since the spacing between the junctions at a given radius now varies linearly with the radius. Stability bounds are, for a radial mesh, necessarily more severe than in the rectilinear case, due to this variation in grid spacing.
), which we expect, since the spacing between the junctions at a given radius now varies linearly with the radius. Stability bounds are, for a radial mesh, necessarily more severe than in the rectilinear case, due to this variation in grid spacing.
Stefan Bilbao
2002-01-22