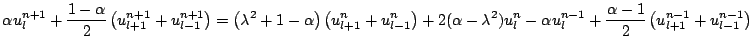A Compact Implicit Scheme

A generalization of scheme (6.33) of an entirely different character is the following:

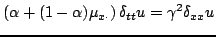$$\left(\alpha + (1-\alpha)\mu_{x\cdot}\right)\delta_{tt}u = \gamma^2\delta_{xx}u$$ (6.66)

This scheme also involves a free parameter 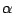$\alpha$, and reduces to scheme (6.33) when 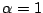$\alpha = 1$, and is again nominally second-order accurate in both space and time. The following recursion results:

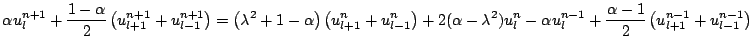$$\alpha u_{l}^{n+1}+\frac{1-\alpha}{2}\left(u_{l+1}^{n+1}+u_{l-1}^... ...n-\alpha u_{l}^{n-1}+\frac{\alpha-1}{2}\left(u_{l+1}^{n-1}+u_{l-1}^{n-1}\right)$$ (6.67)

In this case, the values of the grid function at the update time step 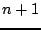$n+1$, written on the left side of the above recursion, are coupled; this is the first instance in this book of a so-called implicit finite difference scheme. It is not possible to solve the above recursion without the use of linear system solution techniques, which are generally more costly than simple explicit updating. In exchange, such schemes are potentially much more accurate than explicit schemes, and often operate under much looser stability conditions.

To this end, it is worth again writing the characteristic polynomial corresponding to scheme (6.66):

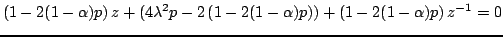$$\left(1-2(1-\alpha)p\right)z+(4\lambda^2 p-2\left(1-2(1-\alpha)p\right))+\left(1-2(1-\alpha)p\right)z^{-1} = 0$$ (6.68)