Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Low-Order Filter Implementations
When latency and time-efficiency is a concern,
the length of the body's impulse response becomes an issue.
Therefore, in these systems, the impulse response
of the body is approximated using lower-order filters and
a modal synthesis model.
To effectively shorten the body's impulse response
for systems requiring low-latency and low-memory needs, methods for removing the peaks
are applied to leave a residual signal and a low-cost representation for the removed
resonating peaks. This reduces the length of the original impulse response while
representing the primary modes parametrically.
The two general approaches for dealing with spectral peak removal include subtraction and
inverse-filtering methods.
The two basic methods are as follows:
- Complex Spectral Subtraction
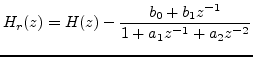 |
(15) |
where 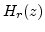 corresponds to the shortened body impulse response while
corresponds to the shortened body impulse response while
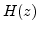 corresponds to the measured body impulse response. The parameters
to be estimated are the second-order filter coefficients
corresponds to the measured body impulse response. The parameters
to be estimated are the second-order filter coefficients 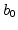 ,
,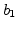 ,
,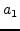 and
and 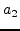 .
.
Complex Spectral Subtraction requires careful estimation of the
phase, amplitude, frequency and bandwidth for peak removal. Furthermore,
the resonators must run in parallel with the residual. Therefore,
advantages obtained from Commuted Synthesis are lost as the approximated
body impulse response model
is not readily commutable with the string component of our physical model [45].
- Inverse-Filtering
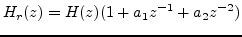 |
(16) |
where 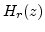 again corresponds to the shortened body impulse response with
again corresponds to the shortened body impulse response with
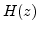 equal to the measured body impulse response. In this form,
the residual signal is readily commutable with the string component of our
physical model as resonators are factored instead of subtracted. Furthermore,
estimating the coefficients of the filter for peak removal requires only
the frequency and bandwidth of the peak and not the amplitude and phase
as is required for Complex Spectral Subtraction [28].
equal to the measured body impulse response. In this form,
the residual signal is readily commutable with the string component of our
physical model as resonators are factored instead of subtracted. Furthermore,
estimating the coefficients of the filter for peak removal requires only
the frequency and bandwidth of the peak and not the amplitude and phase
as is required for Complex Spectral Subtraction [28].
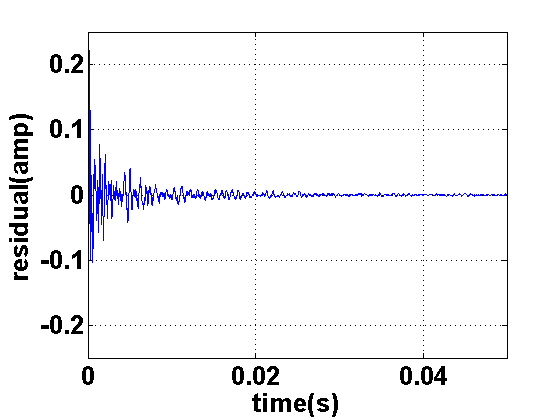
Figure 43:
Time-domain signal of body response with peak at 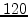 Hz removed.
Hz removed.
|
|
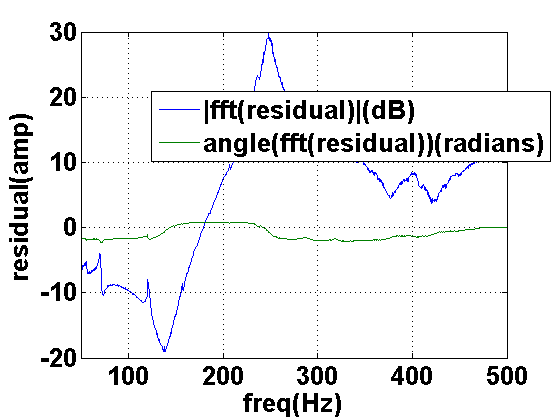
Figure 44:
Spectral view, magnitude and phase, of body response with peak at 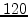 Hz removed. Note that the response is now shorter compared with the original body response in Figure 39.
Hz removed. Note that the response is now shorter compared with the original body response in Figure 39.
|
|
Applying inverse-filtering as described above, we take the original body response
shown in Figures 39 and 40, and remove the peak
centered around 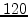 Hz with a bandwidth of
Hz with a bandwidth of 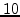 Hz. The residual, shown in Figure 43,
is significantly shorter than the original response. Whereas in Figure 39,
the response lasts for well over
Hz. The residual, shown in Figure 43,
is significantly shorter than the original response. Whereas in Figure 39,
the response lasts for well over 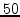 ms, in the residual signal,
its amplitude oscillates near the noise floor at around
ms, in the residual signal,
its amplitude oscillates near the noise floor at around 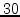 ms. Figure 44 shows
the spectrum, both magnitude and phase, of the response after inverse-filtering. Compared with Figure 41, the peak
at
ms. Figure 44 shows
the spectrum, both magnitude and phase, of the response after inverse-filtering. Compared with Figure 41, the peak
at 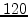 Hz is completely removed.
Hz is completely removed.
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download phys_mod_overview.pdf
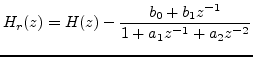
![]() corresponds to the shortened body impulse response while
corresponds to the shortened body impulse response while
![]() corresponds to the measured body impulse response. The parameters
to be estimated are the second-order filter coefficients
corresponds to the measured body impulse response. The parameters
to be estimated are the second-order filter coefficients ![]() ,
,![]() ,
,![]() and
and ![]() .
.
![]() again corresponds to the shortened body impulse response with
again corresponds to the shortened body impulse response with
![]() equal to the measured body impulse response. In this form,
the residual signal is readily commutable with the string component of our
physical model as resonators are factored instead of subtracted. Furthermore,
estimating the coefficients of the filter for peak removal requires only
the frequency and bandwidth of the peak and not the amplitude and phase
as is required for Complex Spectral Subtraction [28].
equal to the measured body impulse response. In this form,
the residual signal is readily commutable with the string component of our
physical model as resonators are factored instead of subtracted. Furthermore,
estimating the coefficients of the filter for peak removal requires only
the frequency and bandwidth of the peak and not the amplitude and phase
as is required for Complex Spectral Subtraction [28].