 |
 |
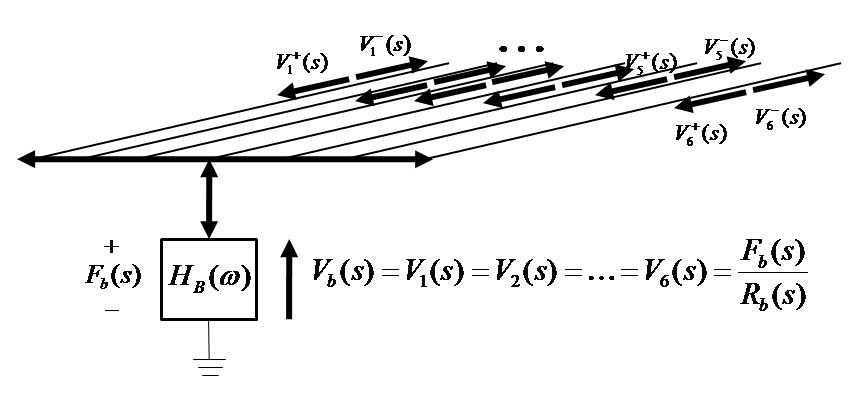
In the physical world, the motion of the string exerts a force on the bridge resulting in a velocity at the point of contact. In Section 2.3.2 from a physical perspective, only energy passing from the string to the body is modeled. However, we can extend our current model to account for not only the influence of the string to the bridge, but also the influence of the bridge to the string. Network theory applied to this junction results in a bi-directional model [24,25,26]. Figure 19 is an illustration of six strings attached to a common bridge. The simplifying assumption is that all strings move at the same velocity as the bridge at the bridge.
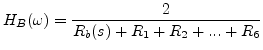 |
Where
![]() , where
, where
![]() is the driving-point admittance
of the bridge and
is the driving-point admittance
of the bridge and ![]() is the wave impedance of string
is the wave impedance of string ![]() . Furthermore, each string's wave impedance
can be computed using its physical characteristics through the following equation:
. Furthermore, each string's wave impedance
can be computed using its physical characteristics through the following equation:
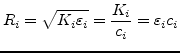 |
where ![]() is the string tension,
is the string tension,
![]() is the string's linear mass density and
is the string's linear mass density and ![]() is the speed at which
waves on the string travel both left and right.
For more information on Network theory and how
it applies to musical acoustics, we refer readers to
http://ccrma.stanford.edu/~jos/pasp/Introduction_Lumped_Models.html.
is the speed at which
waves on the string travel both left and right.
For more information on Network theory and how
it applies to musical acoustics, we refer readers to
http://ccrma.stanford.edu/~jos/pasp/Introduction_Lumped_Models.html.