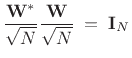Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Lossless Filter Examples
The simplest lossless filter is a unit-modulus gain
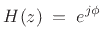 |
(12.82) |
where  can be any phase value. In the real case
can be any phase value. In the real case  can only be 0
or
can only be 0
or 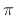 , hence
, hence
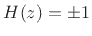 .
.
A lossless FIR filter can only consist of a single nonzero tap:
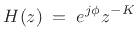 |
(12.83) |
for some fixed integer 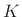 , where
, where  is again some constant phase,
constrained to be 0
or
is again some constant phase,
constrained to be 0
or 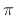 in the real-filter case.
We consider only causal filters here, so
in the real-filter case.
We consider only causal filters here, so 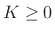 .
.
Every finite-order, single-input, single-output (SISO),
lossless IIR filter (recursive allpass filter) can be written as
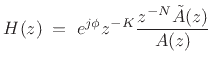 |
(12.84) |
where 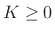 ,
,
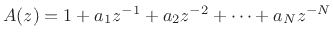 , and
, and
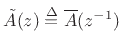 . The polynomial
. The polynomial
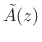 can be obtained by reversing the order of the coefficients in
can be obtained by reversing the order of the coefficients in 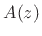 ,
conjugating them, and multiplying by
,
conjugating them, and multiplying by 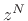 . (The factor
. (The factor  above
serves to restore negative powers of
above
serves to restore negative powers of 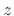 and hence causality.) Such
filters are generally called allpass filters.
and hence causality.) Such
filters are generally called allpass filters.
The normalized DFT matrix is an 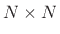 order zero paraunitary
transformation. This is because the normalized DFT matrix,
order zero paraunitary
transformation. This is because the normalized DFT matrix,
![$ \bold{W}=[W_N^{nk}]/\sqrt{N}$](img2190.png) ,
,
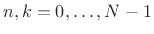 , where
, where
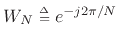 , is a unitary matrix:
, is a unitary matrix:
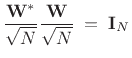 |
(12.85) |
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
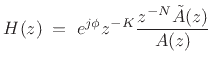
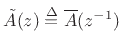 . The polynomial
. The polynomial
![]() order zero paraunitary
transformation. This is because the normalized DFT matrix,
order zero paraunitary
transformation. This is because the normalized DFT matrix,
![]() ,
,
![]() , where
, where
![]() , is a unitary matrix:
, is a unitary matrix: