Next |
Prev |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Overlap-Add (OLA)
STFT Processing
This chapter discusses use of the Short-Time Fourier Transform
(STFT) to implement linear filtering in the frequency domain.
Due to the speed of FFT convolution, the STFT provides the most
efficient single-CPU implementation engine for most FIR filters
encountered in audio signal processing.
Recall from §7.1 the STFT:
where
We noted that if the window 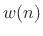 has the
constant overlap-add property
at hop-size
has the
constant overlap-add property
at hop-size 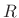 ,
,
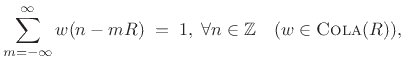 |
(9.2) |
then the sum of the successive DTFTs over time equals the DTFT of the
whole signal 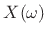 :
:
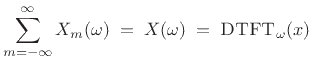 |
(9.3) |
Consequently, the inverse-STFT is simply the inverse-DTFT of this sum:
We may now introduce spectral modifications by multiplying each
spectral frame
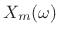 by some filter frequency response
by some filter frequency response
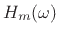 to get
to get
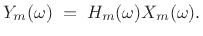 |
(9.4) |
Note that 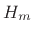 can be different for each frame, giving a certain
class of time-varying filters. The filtered output signal spectrum
is then
can be different for each frame, giving a certain
class of time-varying filters. The filtered output signal spectrum
is then
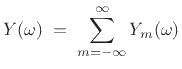 |
(9.5) |
so that
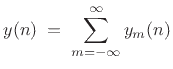 |
(9.6) |
where
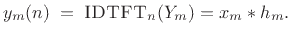 |
(9.7) |
This chapter discusses practical implementation of the above
relations using a Fast Fourier Transform (FFT). In particular, we
use an FFT to compute efficiently what may be regarded as a
sampled DTFT. We will look at how sampling density
must be increased along the unit circle when spectral modifications
are to be performed, and we will discuss further the COLA condition on
the analysis window and hop-size.
In the end, our practical FFT-convolution engine will look as follows:
![$\displaystyle y \eqsp \sum_{m=-\infty}^\infty \hbox{\sc Shift}_{mR} \left( \hbox{\sc FFT}_N^{-1} \left\{ H_m \cdot \hbox{\sc FFT}_N\left[\hbox{\sc Shift}_{-mR}(x)\cdot w_M \right]\right\}\right)$](img1306.png) |
(9.8) |
The sum over 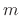 may be interpreted as adding separately filtered
frames
may be interpreted as adding separately filtered
frames
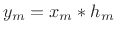 . Due to this filtering, the frames must
overlap, even when the rectangular window is used. As a result, the
overall system is often called an
overlap-add FFT processor,
or
``OLA processor'' for short. It is regarded as a sequence of FFTs
which may be modified, inverse-transformed, and summed. This
``hopping transform'' view of the STFT is the Fourier dual of the
``filter-bank'' interpretation to be discussed in Chapter 9.
. Due to this filtering, the frames must
overlap, even when the rectangular window is used. As a result, the
overall system is often called an
overlap-add FFT processor,
or
``OLA processor'' for short. It is regarded as a sequence of FFTs
which may be modified, inverse-transformed, and summed. This
``hopping transform'' view of the STFT is the Fourier dual of the
``filter-bank'' interpretation to be discussed in Chapter 9.
Subsections
Next |
Prev |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
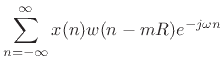

![]() has the
constant overlap-add property
at hop-size
has the
constant overlap-add property
at hop-size ![]() ,
,
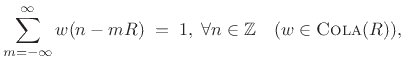
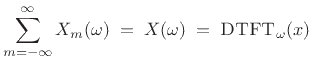
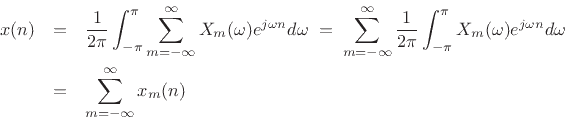
![]() by some filter frequency response
by some filter frequency response
![]() to get
to get
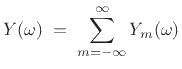
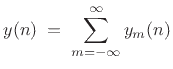
![$\displaystyle y \eqsp \sum_{m=-\infty}^\infty \hbox{\sc Shift}_{mR} \left( \hbox{\sc FFT}_N^{-1} \left\{ H_m \cdot \hbox{\sc FFT}_N\left[\hbox{\sc Shift}_{-mR}(x)\cdot w_M \right]\right\}\right)$](img1306.png)