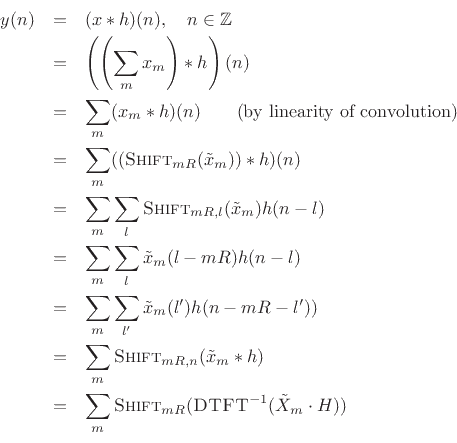
Getting back to acyclic convolution, we may write it as
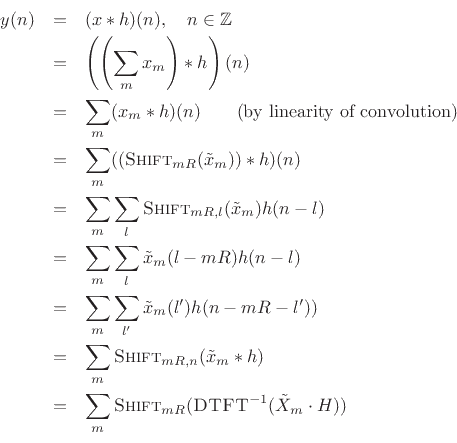
Since
![]() is time limited to
is time limited to
![]() (or
(or
![]() ),
),
![]() can be sampled at intervals of
can be sampled at intervals of
![]() without time aliasing. If
without time aliasing. If ![]() is time-limited to
is time-limited to
![]() , then
, then
![]() will be time limited to
will be time limited to ![]() . Therefore, we may sample
. Therefore, we may sample
![]() at intervals of
at intervals of
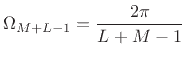 |
(9.22) |
We conclude that practical FFT acyclic convolution may be carried out
using an FFT of any length ![]() satisfying
satisfying
| (9.23) |
![\begin{eqnarray*}
y(n) &=&
\sum_m \hbox{\sc Shift}_{mR,n} \left[\frac{1}{N} \sum_{k=0}^{N-1}
{\tilde H}(\omega_k) {\tilde X}_m(\omega_k) e^{j\omega_k n T}\right]\\
&=&
\sum_m \hbox{\sc Shift}_{mR,n}\left\{ \hbox{\sc IFFT}_N[\hbox{\sc FFT}_N({\tilde x}_m)\cdot \hbox{\sc FFT}_N(h)]\right\},
\end{eqnarray*}](img1426.png)
where
![]() is the length
is the length ![]() DFT of the zero-padded
DFT of the zero-padded
![]() frame
frame
![]() , and
, and
![]() is the length
is the length ![]() DFT of
DFT of ![]() ,
also zero-padded out to length
,
also zero-padded out to length ![]() , with
, with
![]() .
.
Note that the terms in the outer sum overlap when ![]() even if
even if
![]() . In general, an LTI filtering by
. In general, an LTI filtering by ![]() increases
the amount of overlap among the frames.
increases
the amount of overlap among the frames.
This completes our derivation of FFT convolution between an
indefinitely long signal ![]() and a reasonably short FIR filter
and a reasonably short FIR filter
![]() (short enough that its zero-padded DFT can be practically
computed using one FFT).
(short enough that its zero-padded DFT can be practically
computed using one FFT).
The fast-convolution processor we have derived is a special case of the Overlap-Add (OLA) method for short-time Fourier analysis, modification, and resynthesis. See [7,9] for more details.