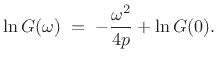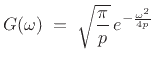Alternate Proof

The Fourier transform of a complex Gaussian can also be derived using the differentiation theorem and its dual (§B.2).^D.1

Proof: Let

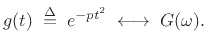$$g(t)\isdefs e^{-pt^2} \;\longleftrightarrow\;G(\omega).$$ (D.19)

Then by the differentiation theorem (§B.2),

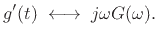$$g^\prime(t) \;\longleftrightarrow\;j\omega G(\omega).$$ (D.20)

By the differentiation theorem dual (§B.3),

$$-jtg(t) \;\longleftrightarrow\;G^\prime(\omega).$$ (D.21)

Differentiating 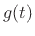$g(t)$ gives

$$g^\prime(t) \eqsp -2ptg(t) \eqsp \frac{2p}{j}[-jtg(t)] \;\longleftrightarrow\;\frac{2p}{j}G^\prime(\omega).$$ (D.22)

Therefore,

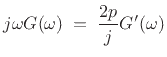$$j\omega G(\omega) \eqsp \frac{2p}{j}G^\prime(\omega)$$ (D.23)

or

$$\left[\ln G(\omega)\right]^\prime \eqsp \frac{G^\prime(\omega)}{G(\omega)} \eqsp -\frac{\omega}{2p} \eqsp \left(-\frac{\omega^2}{4p}\right)^\prime.$$ (D.24)

Integrating both sides with respect to 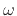$\omega$ yields

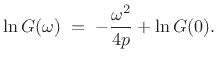$$\ln G(\omega) \eqsp -\frac{\omega^2}{4p} + \ln G(0).$$ (D.25)

In §D.7, we found that $G(0)=\sqrt{\pi/p}$ , so that, finally, exponentiating gives

$$G(\omega) \eqsp \sqrt{\frac{\pi}{p}}\,e^{-\frac{\omega^2}{4p}}$$ (D.26)

as expected.

The Fourier transform of complex Gaussians (``chirplets'') is used in §10.6 to analyze Gaussian-windowed ``chirps'' in the frequency domain.