Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As discussed in [452, p. 362] and exemplified in
§C.17.6, to diagonalize a system, we must find the
eigenvectors of 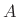 by solving
by solving
for
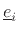 ,
,  , where
, where 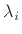 is simply the
is simply the 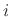 th pole
(eigenvalue of
th pole
(eigenvalue of 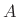 ). The
). The 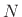 eigenvectors
eigenvectors
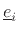 are collected into a
similarity transformation matrix:
are collected into a
similarity transformation matrix:
If there are coupled repeated poles, the corresponding missing
eigenvectors can be replaced by generalized eigenvectors.2.12 The 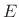 matrix is then used to
diagonalize the system by means of a simple change of
coordinates:
matrix is then used to
diagonalize the system by means of a simple change of
coordinates:
The new diagonalized system is then
where
The transformed system describes the same system as in Eq.(1.8)
relative to new state-variable coordinates
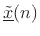 . For example,
it can be checked that the transfer-function matrix is unchanged.
. For example,
it can be checked that the transfer-function matrix is unchanged.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() by solving
by solving