State Transformations

In previous work, time-domain adaptors (digital filters) converting between K variables and W variables have been devised [224]. In this section, an alternative approach is proposed. Mapping Eq.(E.7) gives us an immediate conversion from W to K state variables, so all we need now is the inverse map for any time $n$ . This is complicated by the fact that non-local spatial dependencies can go indefinitely in one direction along the string, as we will see below. We will proceed by first writing down the conversion from W to K variables in matrix form, which is easy to do, and then invert that matrix. For simplicity, we will consider the case of an infinitely long string.

To initialize a K variable simulation for starting at time $n+1$ , we need initial spatial samples at all positions $m$ for two successive times $n-1$ and $n$ . From this state specification, the FDTD scheme Eq.(E.3) can compute $y(n+1,m)$ for all $m$ , and so on for increasing $n$ . In the DW model, all state variables are defined as belonging to the same time $n$ , as shown in Fig.E.2.

Figure E.2: DW flow diagram.

From Eq.(E.6), and referring to the notation defined in Fig.E.2, we may write the conversion from W to K variables as

$$y_{n,m+1} = y^{+}_{n,m+1}+ y^{-}_{n,m+1}$$

$$y_{n,m-1} = y^{+}_{n,m-1}+ y^{-}_{n,m-1}$$

$$y_{n-1,m} = y^{+}_{n-1,m}+ y^{-}_{n-1,m}$$

$$= y^{+}_{n,m+1}+ y^{-}_{n,m-1} \protect$$ (E.8)

where the last equality follows from the traveling-wave behavior (see Fig.E.2).

Figure E.3: Stencil of the FDTD scheme.

Figure E.3 shows the so-called ``stencil'' of the FDTD scheme. The larger circles indicate the state at time $n$ which can be used to compute the state at time $n+1$ . The filled and unfilled circles indicate membership in one of two interleaved grids [55]. To see why there are two interleaved grids, note that when $m$ is even, the update for $y_{n+1,m}$ depends only on odd $m$ from time $n$ and even $m$ from time $n-1$ . Since the two W components of $y_{n-1,m}$ are converted to two W components at time $n$ in Eq.(E.8), we have that the update for $y_{n+1,m}$ depends only on W components from time $n$ and positions $m\pm1$ . Moving to the next position update, for $y_{n+1,m+1}$ , the state used is independent of that used for $y_{n+1,m}$ , and the W components used are from positions $m$ and $m+2$ . As a result of these observations, we see that we may write the state-variable transformation separately for even and odd $m$ , e.g.,

$$\left[\! \begin{array}{c} \vdots \\ y_{n,m-1}\\ y_{n-1,m}\\ y_{n,m+1}\\ y_{n-1,m+2}\\ y_{n,m+3}\\ y_{n-1,m+4}\\ y_{n,m+5}\\ \vdots \\ \end{array} \!\right] \!=\! \left[\! \begin{array}{cccccccccc} \ddots & & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & 0 \\ \cdots & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & \cdots\\ 0 & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{array} \!\right] \left[\! \begin{array}{c} \vdots \\ y^{+}_{n,m-1}\\ y^{-}_{n,m-1}\\ y^{+}_{n,m+1}\\ y^{-}_{n,m+1}\\ y^{+}_{n,m+3}\\ y^{-}_{n,m+3}\\ y^{+}_{n,m+5}\\ y^{-}_{n,m+5}\\ \vdots \end{array} \!\right]. \protect$$ (E.9)

Denote the linear transformation operator by $\mathbf{T}$ and the K and W state vectors by $\underline{x}_K$ and $\underline{x}_W$ , respectively. Then Eq.(E.9) can be restated as

$$\underline{x}_K= \mathbf{T}\underline{x}_W. \protect$$ (E.10)

The operator $\mathbf{T}$ can be recognized as the Toeplitz operator associated with the linear, shift-invariant filter $H(z)=1+z^{-1}$ . While the present context is not a simple convolution since $\underline{x}_W$ is not a simple time series, the inverse of $\mathbf{T}$ corresponds to the Toeplitz operator associated with

$$H(z) = \frac{1}{1+z^{-1}} = 1 - z^{-1}+ z^{-2} - z^{-3} + \cdots.$$

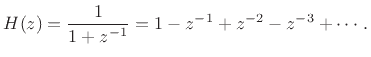
Therefore, we may easily write down the inverted transformation:

$$\left[\! \begin{array}{c} \vdots \\ y^{+}_{n,m-1}\\ y^{-}_{n,m-1}\\ y^{+}_{n,m+1}\\ y^{-}_{n,m+1}\\ y^{+}_{n,m+3}\\ y^{-}_{n,m+3}\\ y^{+}_{n,m+5}\\ y^{-}_{n,m+5}\\ \vdots \end{array} \!\right] \!=\! \left[\! \begin{array}{crrrrrrrrc} \ddots & & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \pm1 \\ \cdots & 1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 & \cdots\\ \cdots & 0 & 1 & -1 & 1 & -1 & 1 & -1 & 1 & \cdots\\ \cdots & 0 & 0 & 1 & -1 & 1 & -1 & 1 & -1 & \cdots\\ \cdots & 0 & 0 & 0 & 1 & -1 & 1 & -1 & 1 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 1 & -1 & 1 & -1 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 1 & -1 & 1 & \cdots\\ \cdots & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & \cdots\\ 0 & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{array} \!\right] \!\! \left[\! \begin{array}{c} \vdots \\ y_{n,m-1}\\ y_{n-1,m}\\ y_{n,m+1}\\ y_{n-1,m+2}\\ y_{n,m+3}\\ y_{n-1,m+4}\\ y_{n,m+5}\\ \vdots \\ \end{array} \!\right] \protect$$ (E.11)

The case of the finite string is identical to that of the infinite string when the matrix $\mathbf{T}$ is simply ``cropped'' to a finite square size (leaving an isolated 1 in the lower right corner); in such cases, $\mathbf{T}^{-1}$ as given above is simply cropped to the same size, retaining its upper triangular $\pm 1$ structure. Another interesting set of cases is obtained by inserting a 1 in the lower-left corner of the cropped $\mathbf{T}$ matrix to make it circulant; in these cases, the $M\times M$ matrix $\mathbf{T}^{-1}$ contains $\pm1/2$ in every position for even $M$ , and is singular for odd $M$ (when there is one zero eigenvalue).