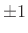Half-Rate Ladder Waveguide Filters

The delays preceding the two inputs to each scattering junction can be ``pushed'' into the junction and then ``pulled'' out to the outputs and combine with the delays there. (This is easy to show using the Kelly-Lochbaum scattering junction derived in §C.8.4.) By performing this operation on every other section in the DWF chain, the half-rate ladder waveguide filter shown in Fig.C.25 is obtained [436].

Figure: Half-rate ladder waveguide filter (cf. Fig.C.24).

This ``half-rate'' ladder DWF is so-called because its sampling rate can be cut in half due to each delay being two-samples long. It has advantages worth considering, which will become clear after we have derived conventional ladder digital filters below. Note that now pairs of scattering junctions can be computed in parallel, and an exact physical interpretation remains. That is, it can still be used as a general purpose physical modeling building block in this more efficient (half-rate) form.

Note that when the sampling rate is halved, the physical wave variables (computed by summing two traveling-wave components) are at the same time only every other spatial sample. In particular, the physical transverse forces on the right side of scattering junctions $i$ and $i+1$ in Fig.C.25 are

$$\begin{eqnarray*} f_i(t+T)&=&f^{{+}}_i(t+T)+f^{{-}}_i(t+T)\\ [5pt] f_{i+1}(t)&=&f^{{+}}_{i+1}(t)+f^{{-}}_{i+1}(t) \end{eqnarray*}$$

respectively. In the half-rate case, adjacent spatial samples are separated in time by half a temporal sample $T/2$ . If physical variables are needed only for even-numbered (or odd-numbered) spatial samples, then there is no relative time skew, but more generally, things like collision detection, such as for slap-bass string-models (§9.1.6), can be affected. In summary, the half-rate ladder waveguide filter has an alternating half-sample time skew from section to section when used as a physical modeling building block.