Stick Diagram Design

When designing a filter with a prescribed magnitude response by the Bode ``stick diagram'' method, we think in terms of poles and zeros ``breaking'' at certain frequencies. For example, in the term

$$H_n(j\omega) = \frac{-p_n}{j\omega-p_n}$$

which is scaled to have unity gain at $\omega=0$ , the pole is said to ``break'' at frequency $\omega=\vert p_n\vert$ . This is easily seen to be the $-3$ dB point of the term, since

$$H_n(jp_n) = \frac{-p_n}{j (\pm p_n)-p_n} = \frac{1}{1\pm j}$$

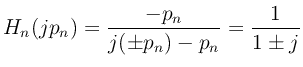
which has magnitude $1/\sqrt{2} \approx -3$ dB. Thus, the gain of the term is approximately constant out to $\omega=\vert p_n\vert$ , where it reaches its $-3$ dB, or ``half power'' frequency, followed by its asymptotic roll-off of $-6$ dB per octave. A zero term $H_m(j\omega) = (j\omega-z_m)/(-z_m) = 1-j\omega/z_m$ similarly starts out flat, reaches magnitude-gain $+3$ dB at its break frequency $\omega=\vert z_m\vert$ , and asymptotically approaches $+6$ dB per octave for $\omega\gg \vert z_m\vert$ .

The Bode design procedure is then to start at dc ($\omega=0$ ) and map out break-frequencies for poles and zeros so as to follow the desired response as closely as desired. Since this tool is commonly applied in control-system design, there is also usually consideration for the phase plot as well, which has similarly simple behavior.¹⁷

The basic Bode ``stick diagram'' consists only of straight line segments, each having slope given by some integer number of nepers per neper (or integer multiple of $\pm 6$ dB/octave, etc.), with the knowledge that the actual response will be a smoothed version of the stick diagram, traversing the $\pm 3$ dB points at line-segment intersections corresponding to isolated breaking zeros and poles, respectively.