As mentioned in the introduction to this chapter, it takes many sinusoidal components to synthesize noise well (as many as 25 per critical band of hearing under certain conditions [85]). When spectral peaks are that dense, they are no longer perceived individually, and it suffices to match only their statistics to a perceptually equivalent degree.
Sines+Noise (S+N) synthesis [249] generalizes the
sinusoidal signal models to include a filtered noise component,
as depicted in Fig.10.7. In that figure, white noise is
denoted by ![]() , and the slowly changing linear filter applied to
the noise at time
, and the slowly changing linear filter applied to
the noise at time ![]() is denoted
is denoted
![]() .
.
The time-varying spectrum of the signal is said to be made up of a deterministic component (the sinusoids) and a stochastic component (time-varying filtered noise) [246,249]:
![$\displaystyle s(t) \eqsp \sum_{i=1}^{N} A_i(t) \cos[ \theta_i(t)] + e(t),$](img1824.png) |
(11.21) |
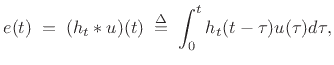 |
(11.22) |
Filtering white-noise to produce a desired timbre is an example of subtractive synthesis [186]. Thus, additive synthesis is nicely supplemented by subtractive synthesis as well.