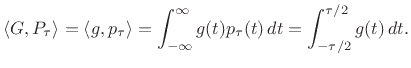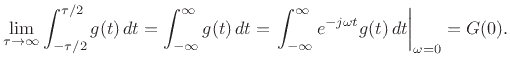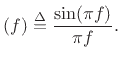Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
The preceding Fourier pair can be used to show that
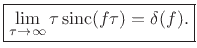 |
(B.35) |
Proof: The inverse Fourier transform of
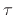 sinc
sinc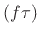 is
is
In particular, in the middle of the rectangular pulse at 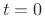 , we have
, we have
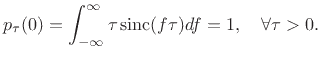 |
(B.36) |
This establishes that the algebraic area under
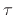 sinc
sinc is
1 for every
is
1 for every 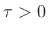 . Every delta function (impulse) must have this
property.
. Every delta function (impulse) must have this
property.
We now show that
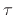 sinc
sinc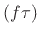 also satisfies the sifting
property in the limit as
also satisfies the sifting
property in the limit as
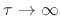 . This property fully
establishes the limit as a valid impulse. That is, an impulse
. This property fully
establishes the limit as a valid impulse. That is, an impulse
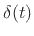 is any function having the property that
is any function having the property that
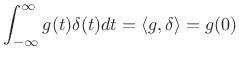 |
(B.37) |
for every continuous function 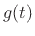 . In the present case, we need to
show, specifically, that
. In the present case, we need to
show, specifically, that
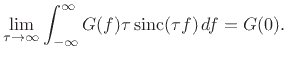 |
(B.38) |
Define
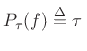 sinc
sinc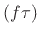 . Then by the power theorem
(§B.9),
. Then by the power theorem
(§B.9),
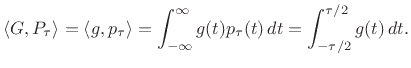 |
(B.39) |
Then as
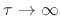 , the limit converges to the algebraic area
under
, the limit converges to the algebraic area
under 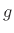 , which is
, which is 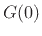 as desired:
as desired:
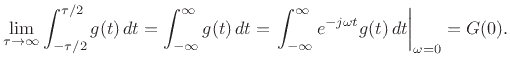 |
(B.40) |
We have thus established that
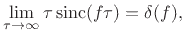 |
(B.41) |
where
sinc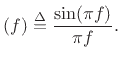 |
(B.42) |
For related discussion, see [36, p. 127].
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() sinc
sinc![]() is
is
![\begin{eqnarray*}
p_\tau(t)
&=& \ensuremath{\int_{-\infty}^{\infty}}\tau\,\mbox{sinc}\left(\frac{\omega}{2\pi}\tau\right) e^{j\omega t}\frac{d\omega}{2\pi}\\
&=& \ensuremath{\int_{-\infty}^{\infty}}\tau\,\mbox{sinc}(f\tau) e^{j2\pi f t}df\\
&=& \left\{\begin{array}{ll}
1, & \left\vert\tau\right\vert\leq 1/2 \\ [5pt]
0, & \mbox{otherwise}. \\
\end{array} \right.
\end{eqnarray*}](img2467.png)
![]() , we have
, we have
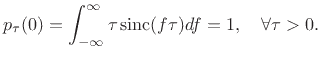
![]() sinc
sinc![]() also satisfies the sifting
property in the limit as
also satisfies the sifting
property in the limit as
![]() . This property fully
establishes the limit as a valid impulse. That is, an impulse
. This property fully
establishes the limit as a valid impulse. That is, an impulse
![]() is any function having the property that
is any function having the property that
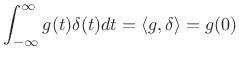
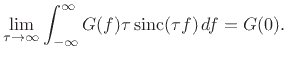
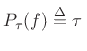 sinc
sinc