Recall from §5.4 that the frequency-domain image of a
sinusoid ``through a window'' is the window transform scaled by the
sinusoid's amplitude and shifted so that the main lobe is centered
about the sinusoid's frequency. A spectrum analysis of two sinusoids
summed together is therefore, by linearity of the Fourier transform,
the sum of two overlapping window transforms, as shown in
Fig.5.12 for the rectangular window. A simple
sufficient requirement for resolving two sinusoidal
peaks spaced ![]() Hz apart is to choose a window length long
enough so that the main lobes are clearly separated when the
sinusoidal frequencies are separated by
Hz apart is to choose a window length long
enough so that the main lobes are clearly separated when the
sinusoidal frequencies are separated by ![]() Hz. For example, we
may require that the main lobes of any Blackman-Harris window meet at
the first zero crossings in the worst case (narrowest frequency
separation); this is shown in Fig.5.12 for the rectangular-window.
Hz. For example, we
may require that the main lobes of any Blackman-Harris window meet at
the first zero crossings in the worst case (narrowest frequency
separation); this is shown in Fig.5.12 for the rectangular-window.
To obtain the separation shown in Fig.5.12, we must have
![]() Hz, where
Hz, where ![]() is the main-lobe width in Hz, and
is the main-lobe width in Hz, and
![]() is the minimum sinusoidal frequency separation in Hz.
is the minimum sinusoidal frequency separation in Hz.
For members of the ![]() -term Blackman-Harris window family,
-term Blackman-Harris window family, ![]() can
be expressed as
can
be expressed as
![]() , as indicated by
Table 5.1. In normalized radian frequency units, i.e.,
radians per sample, we have
, as indicated by
Table 5.1. In normalized radian frequency units, i.e.,
radians per sample, we have
![]() . For comparison, Table 5.2 lists minimum effective
values of
. For comparison, Table 5.2 lists minimum effective
values of ![]() for each window (denoted
for each window (denoted ![]() ) given by an
empirically verified sharper lower bound on the value needed for
accurate peak-frequency measurement [1], as discussed
further in §5.5.4 below.
) given by an
empirically verified sharper lower bound on the value needed for
accurate peak-frequency measurement [1], as discussed
further in §5.5.4 below.
|
We make the main-lobe width ![]() smaller by increasing the window
length
smaller by increasing the window
length ![]() . Specifically, requiring
. Specifically, requiring
![]() Hz implies
Hz implies
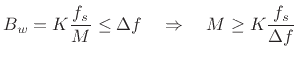 |
(6.26) |