Many signals are periodic in nature, such as short segments of
most tonal musical instruments and speech. The sinusoidal components
in a periodic signal are constrained to be harmonic, that is,
occurring at frequencies that are an integer multiple of the
fundamental frequency ![]() .6.6 Physically, any ``driven
oscillator,'' such as bowed-string instruments, brasses, woodwinds,
flutes, etc., is usually quite periodic in normal steady-state
operation, and therefore generates harmonic overtones in steady
state. Freely vibrating resonators, on the other hand, such as
plucked strings, gongs, and ``tonal percussion'' instruments,
are not generally periodic.6.7
.6.6 Physically, any ``driven
oscillator,'' such as bowed-string instruments, brasses, woodwinds,
flutes, etc., is usually quite periodic in normal steady-state
operation, and therefore generates harmonic overtones in steady
state. Freely vibrating resonators, on the other hand, such as
plucked strings, gongs, and ``tonal percussion'' instruments,
are not generally periodic.6.7
Consider a periodic signal with fundamental frequency ![]() Hz.
Then the harmonic components occur at integer multiples of
Hz.
Then the harmonic components occur at integer multiples of ![]() , and
so they are spaced in frequency by
, and
so they are spaced in frequency by
![]() . To resolve
these harmonics in a spectrum analysis, we require, adapting
(5.27),
. To resolve
these harmonics in a spectrum analysis, we require, adapting
(5.27),
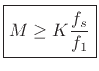 |
(6.28) |
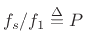 is the fundamental period of the signal in samples.
Thus, another way of stating our simple, sufficient resolution
requirement on window length
is the fundamental period of the signal in samples.
Thus, another way of stating our simple, sufficient resolution
requirement on window length
Specifically, resolving the harmonics of a periodic signal with period
![]() samples is assured if we have at least
samples is assured if we have at least
![\begin{figure*}\centering
\subfigure[Length $M=100$\ rectangular window]{
\epsfxsize =\twidth
\epsfysize =1.5in \epsfbox{eps/EffectiveLength1.eps}
}
\subfigure[Length $M=200$\ Hamming window]{
\epsfxsize =\twidth
\epsfysize =1.5in \epsfbox{eps/EffectiveLength2.eps}
}
\subfigure[Length $M=300$\ Blackman window]{
\epsfxsize =\twidth
\epsfysize =1.5in \epsfbox{eps/EffectiveLength3.eps}
}\end{figure*}](img1000.png) |