Repeat (Scaling) Operator

We define the repeat operator in the frequency domain as a scaling of frequency axis by some integer factor $L>0$ :

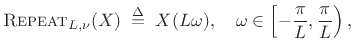$$\hbox{\sc Repeat}_{L,\nu}(X) \isdefs X(L\omega), \quad \omega\in\left[-\frac{\pi}{L},\frac{\pi}{L}\right),$$ (3.30)

where $\nu=L\omega\in[-\pi,\pi)$ denotes the radian frequency variable after applying the repeat operator.

The repeat operator maps the entire unit circle (taken as $-\pi$ to $\pi$ ) to a segment of itself $[-\pi/L,\pi/L)$ , centered about $\omega = 0$ , and repeated $L$ times. This is illustrated in Fig.2.2 for $L=3$ .

Since the frequency axis is continuous and $2\pi$ -periodic for DTFTs, the repeat operator is precisely equivalent to a scaling operator for the Fourier transform case (§B.4). We call it ``repeat'' rather than ``scale'' because we are restricting the scale factor to positive integers, and because the name ``repeat'' describes more vividly what happens to a periodic spectrum that is compressively frequency-scaled over the unit circle by an integer factor.