The scaling theorem (or similarity theorem) provides
that if you horizontally ``stretch'' a signal by the factor ![]() in the time domain, you ``squeeze'' and amplify its Fourier transform
by the same factor in the frequency domain. This is an important
general Fourier duality relationship.
in the time domain, you ``squeeze'' and amplify its Fourier transform
by the same factor in the frequency domain. This is an important
general Fourier duality relationship.
Theorem: For all continuous-time functions ![]() possessing a Fourier
transform,
possessing a Fourier
transform,
| (B.9) |
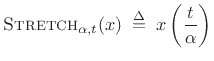 |
(B.10) |
 |
(B.11) |
Proof:
Taking the Fourier transform of the stretched signal gives

The absolute value appears above because, when ![]() ,
,
![]() , which brings out a minus sign in front of the
integral from
, which brings out a minus sign in front of the
integral from ![]() to
to ![]() .
.