Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As shown in §B.14 above, the Fourier transform of an impulse
train is an impulse train with inversely proportional spacing:
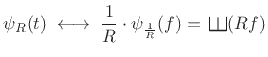 |
(B.56) |
where
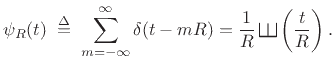 |
(B.57) |
Using this Fourier theorem, we can derive the continuous-time PSF using the
convolution theorem for Fourier transforms:B.1
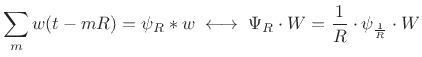 |
(B.58) |
Using linearity and the shift theorem for inverse Fourier
transforms, the above relation yields
We have therefore shown
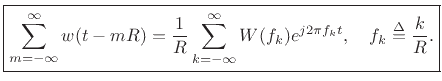 |
(B.59) |
Compare this result to Eq.(8.30). The left-hand side of (B.60)
can be interpreted
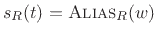 , i.e., the time-alias of
, i.e., the time-alias of 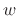 on
a block of length
on
a block of length 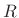 . The function
. The function 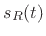 is periodic with period
is periodic with period
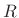 seconds. The right-hand side of (B.60) can be interpreted as
the inverse Fourier series of
seconds. The right-hand side of (B.60) can be interpreted as
the inverse Fourier series of 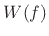 sampled at intervals of
sampled at intervals of 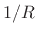 Hz. This sampling of
Hz. This sampling of 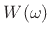 in the frequency domain corresponds to the aliasing of
in the frequency domain corresponds to the aliasing of 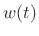 in the
time domain.
in the
time domain.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
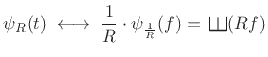
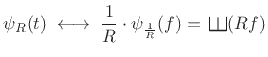
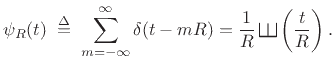
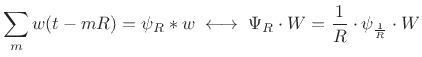
![\begin{eqnarray*}
\sum_m w(t-mR)
&=& \frac{1}{R} \hbox{\sc IFT}_t
\left[W(f)\sum_k\delta\left(f-k\frac{1}{R}\right) \right]
\quad\left(\mbox{define $f_k\isdef \frac{k}{R}$}\right)
\\ [5pt]
&=& \frac{1}{R} \hbox{\sc IFT}_t
\left[\sum_k W(f_k)\cdot\delta\left(f-f_k\right) \right]\\ [5pt]
&=& \frac{1}{R}
\sum_k W(f_k)\cdot\hbox{\sc IFT}_t \left[\delta\left(f-f_k\right) \right]\\ [5pt]
&=& \frac{1}{R} \sum_k W(f_k)e^{j 2\pi f_k t}.
\end{eqnarray*}](img2521.png)