Perfect Reconstruction Filter Banks

We now consider filter banks with an arbitrary number of channels, and ask under what conditions do we obtain a perfect reconstruction filter bank? Polyphase analysis will give us the answer readily. Let's begin with the $N$ -channel filter bank in Fig.11.20. The downsampling factor is $R\leq N$ . For critical sampling, we set $R=N$ .

Figure: $N$ -channel filter bank.

The next step is to expand each analysis filter $H_k(z)$ into its $N$ -channel ``type I'' polyphase representation:

$$H_k(z) \eqsp \sum_{l=0}^{N-1} z^{-l} E_{kl}(z^N)$$ (12.49)

or

$$\underbrace{\left[\begin{array}{c} H_0(z) \\ [2pt] H_1(z) \\ [2pt] \vdots \\ [2pt] \!\!H_{N-1}(z)\!\!\end{array}\right]}_{\bold{h}(z)} = \underbrace{\left[\begin{array}{cccc} E_{0,0}(z^N) & E_{0,1}(z^N) & \cdots & E_{0,N-1}(z^N) \\ E_{1,0}(z^N) & E_{1,1}(z^N) & \cdots & E_{1,N-1}(z^N)\\ \vdots & \vdots & \cdots & \vdots\\ \!\!E_{N-1,0}(z^N) & E_{N-1,1}(z^N) & \cdots & E_{N-1,N-1}(z^N) \!\! \end{array}\right]}_{\bold{E}(z^N)} \underbrace{\left[\begin{array}{c} 1 \\ [2pt] z^{-1} \\ [2pt] \vdots \\ [2pt] \!\!z^{-(N-1)}\!\!\end{array}\right]}_{\bold{e}(z)}$$ (12.50)

which we can write as

$$\bold{h}(z) \eqsp \bold{E}(z^N)\bold{e}(z).$$ (12.51)

Similarly, expand the synthesis filters in a type II polyphase decomposition:

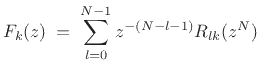$$F_k(z) \eqsp \sum_{l=0}^{N-1} z^{-(N-l-1)}R_{lk}(z^N)$$ (12.52)

or

$$\underbrace{\left[\begin{array}{c} F_0(z) \\ [2pt] F_1(z) \\ [2pt] \vdots \\ [2pt] \!\!F_{N-1}(z)\!\!\end{array}\right]^T}_{\bold{f}^T(z)} \eqsp \underbrace{\left[\begin{array}{c} \!\!z^{-(N-1)}\!\! \\ [2pt] \!\!z^{-(N-2)}\!\! \\ [2pt] \vdots \\ [2pt] 1\end{array}\right]^T}_{{\tilde{\bold{e}}}(z)} \underbrace{\left[\begin{array}{cccc} R_{0,0}(z^N) & R_{0,1}(z^N) & \cdots & R_{0,N-1}(z^N) \\ R_{1,0}(z^N) & R_{1,1}(z^N) & \cdots & R_{1,N-1}(z^N)\\ \vdots & \vdots & \cdots & \vdots\\ \!\!R_{N-1,0}(z^N) & R_{N-1,1}(z^N) & \cdots & R_{N-1,N-1}(z^N)\!\! \end{array}\right]}_{\bold{R}(z^N)}$$ (12.53)

which we can write as

$$\bold{f}^T(z) \eqsp {\tilde{\bold{e}}}(z)\bold{R}(z^N).$$ (12.54)

The polyphase representation can now be depicted as shown in Fig.11.21. When $R=N$ , commuting the up/downsamplers gives the result shown in Fig.11.22. We call $\bold{E}(z)$ the polyphase matrix.

Figure: Polyphase representation of the $N$ -channel filter bank.

Figure: Efficient polyphase form of the $N$ -channel filter bank.

As we will show below, the above simplification can be carried out more generally whenever $R$ divides $N$ (e.g., $R=N/2, N/3,\ldots, 1$ ). In these cases $\bold{E}(z)$ becomes $\bold{E}(z^{N/R})$ and $\bold{R}(z)$ becomes $\bold{R}(z^{N/R})$ .