Necessary and Sufficient Conditions for Perfect Reconstruction

It can be shown [287] that the most general conditions for perfect reconstruction are that

$$\zbox {\bold{R}(z)\bold{E}(z) \eqsp c z^{-K} \left[\begin{array}{cc} \bold{0}_{(N-L)\times L} & z^{-1}\bold{I}_{N-L} \\ [2pt] \bold{I}_L & \bold{0}_{L \times (N-L)} \end{array}\right]}$$ (12.63)

for some constant 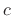$c$ and some integer 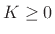$K\geq 0$ , where $L$ is any integer between 0 and $N-1$ .

Note that the more general form of 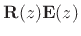$\bold{R}(z)\bold{E}(z)$ above can be regarded as a (non-unique) square root of a vector unit delay, since

$$\left[\begin{array}{cc} \bold{0}_{(N-L)\times L} & z^{-1}\bold{I}_{N-L} \\ [2pt] \bold{I}_L & \bold{0}_{L \times (N-L)} \end{array}\right]^2 \eqsp z^{-1}\bold{I}_N.$$ (12.64)

Thus, the general case is the same thing as

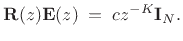$$\bold{R}(z)\bold{E}(z) \eqsp c z^{-K} \bold{I}_N.$$ (12.65)

except for some channel swapping and an extra sample of delay in some channels.